Высшая математика (аналитическая геометрия, линейная алгебра, функции и пределы): Учебно-методическое пособие

 Министерство образования Республики Беларусь

Учреждение образования «Международный государственный экологический университет имени А.Д. Сахарова»

ВЫСШАЯ МАТЕМАТИКА

(аналитическая геометрия, линейная алгебра, функции и пределы)

Минск 2008

ББК 22.11я73

УДК 51(076.1)

С 71

Авторы-составители: Е.П. Борботко, старший преподаватель

                                    кафедры физики и высшей математики МГЭУ

                                    им. А.Д.Сахарова;

     Т.Е. Кузьменкова, кандидат

                                    педагогических наук, доцент кафедры физики и

                                    высшей математики МГЭУ им. А.Д. Сахарова;

      А.В.Шевцова, старший преподаватель

      кафедры физики и высшей математики МГЭУ

      им. А.Д. Сахарова.

      Рецензенты:

Печатается по решению научно-методического совета

Учреждения образования «Международный государственный экологический университет им. А.Д. Сахарова»

Высшая математика (матрицы и определители, аналитическая геометрия, линейная алгебра, функции и пределы): Учеб.-метод. пособие /Сост.: Е.П.Борботко, Т.Е. Кузьменкова, А.В.Шевцова,–  Минск: -,2008. – с.

Пособие предназначено для студентов заочного отделения факультета экологической медицины и содержит контрольную работу по высшей математике, необходимый теоретический материал к каждому разделу контрольной работы.

                                                                                                          ББК 22.11я73

УДК 51(076.1)

Предисловие

Первая контрольная работа выполняется по следующим разделам высшей математики:

1. Векторная алгебра

Координаты и длина вектора. Скалярное, векторное и смешанное произведение: определение и вычисление. Угол между векторами. Признаки параллельности и перпендикулярности векторов. Площадь параллелограмма и треугольника. Объем пирамиды, построенной на векторах. Признак компланарности векторов.

2. Аналитическая геометрия на плоскости

Различные виды уравнений прямой на плоскости. Угол между прямыми. Признаки параллельности и перпендикулярности прямых.

Уравнение окружности. Эллипс, гипербола, парабола (определение, канонические уравнения).

3. Аналитическая геометрия в пространстве

Способы задания плоскости в пространстве. Общее уравнение плоскости. Способы задания прямой в пространстве. Угол между плоскостями, прямыми, прямой и плоскостью. Признаки параллельности и перпендикулярности плоскостей, прямых, прямой и плоскости.

4. Элементы линейной алгебры

Матрицы. Действия над матрицами. Определители 2-го и 3-го порядка. Обратная матрица. Решение системы линейных уравнений методом Гаусса, по формулам Крамера и матричным способом.

5. Предел и непрерывность функции

Функции и их свойства. Способы задания функций. Предел функции. 1-й и 2-й замечательные пределы. Раскрытие неопределенностей вида

  ,   ,   ,   ,   .

Непрерывность функции. Точки разрыва. Односторонние пределы.

1.1 Матрицы и определители

Матрицей называется прямоугольная таблица, составленная из действительных или комплексных чисел:

.

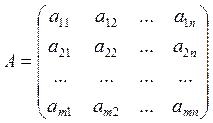Горизонтальные ряды чисел матрицы называются ее строками, а вертикальные- столбцами. Числа  называются элементами матрицы, где i – номер строки, j – номер столбца.  Матрицу,  имеющую  строк и столбцов, называют матрицей размеров . Если , то матрица называется квадратной порядка .

          Определителем квадратной матрицы 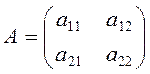 называется число:  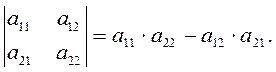Это определитель второго порядка.

          Аналогично, определителем третьего порядка называется число:

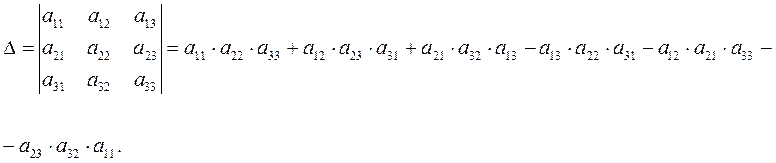
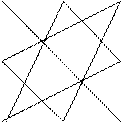
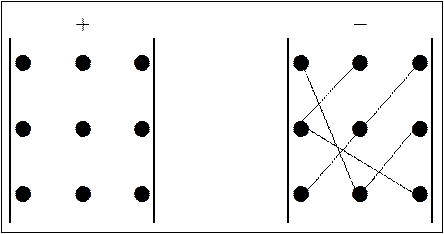
       При вычислении определителя пользуются правилом треугольника, которое схематически выглядит следующим образом:

1.2. Действия над матрицами

Сложение матриц.

Пусть заданы две матрицы одинаковых размеров : и . Их суммой A+B называется матрица размеров  , такая, что , ; . Другими словами, при сложении матриц их соответствующие элементы складываются.

Произведение матрицы на число.

Произведением матрицы  размеров на число α (или числа α на матрицу ) называется матрица  размеров , такая, что , ; . Произведение матрицы A на число α обозначается Aα или αA.

Разность матриц A-Bопределим следующим образом: A-B=A+(-B).

Произведение матриц.

Матрицу A будем называть согласованной с матрицей B, если число столбцов матрицы  Aравно числу строк матрицы B. (Из согласованности матрицы A с B не следует, вообще говоря, согласованность матрицы B с A. )

Произведение матрицы A на матрицу B вводится только тогда, когда матрица A согласована с матрицей B, т.е. если A есть матрица размеров , а B –размеров .

Произведением матрицы  на матрицу  называется матрица  размеров , такая, что .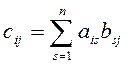

Произведение матрицы A на матрицу B обозначается AB.

Из определения следует, что элемент матрицы AB, стоящий в i–й строке и j–м столбце, равен сумме произведений элементов i–й строки матрицы A на соответствующие элементы j–го столбца матрицы B.

Произведение AB часто называют произведением матрицы A на матрицу B справа или произведением матрицы B на матрицу A слева.

Если произведение AB существует, то произведение BA, вообще говоря, не существует. Если ABи BA существуют, то возможно, .

Если , то матрицы называются перестановочными или коммутирующими.

1.3. Обратная матрица

Если для матрицы А существует матрица В, такая, что , где Е- единичная матрица, то матрица В называется обратной к матрице А.

Из определения следует, что Аи В – квадратные матрицы одинакового порядка. Матрицу, обратную к матрице А, будем обозначать А^-1.

Невырожденной или неособенной матрицей называется квадратная матрица, определитель которой отличен от нуля. Если определитель матрицы равен нулю, то матрица называется вырожденной или особенной.

Для того, чтобы существовала матрица В, обратная матрице А, необходимо и достаточно, чтобы матрица А была невырожденной.

Определитель второго порядка, который получается из определителя  третьего  порядка вычеркиванием  -й строки и -го столбца, называется минором элемента  определителя  и обозначается .

Алгебраическим дополнением  элемента  определителя  называется минор , взятый со знаком , обозначается .

Итак, .

Обратная к данной матрица может быть получена следующим образом

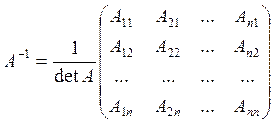, где

- определитель матрицы А, - алгебраические дополнения элементов матрицы А.

Примеры решения задач

Задача 1. Найти сумму и разность матриц Aи B, а так же произведение матрицы A на число α=-3.

,  .

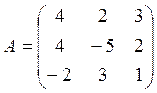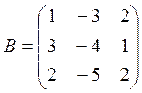Решение.  Матрицы Aи B имеют одинаковые размеры, следовательно, для них определена операция сложения (вычитания). Найдем сумму матриц

.

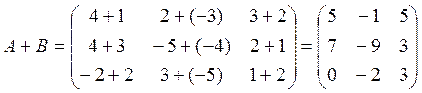Разность матриц будет равна

.

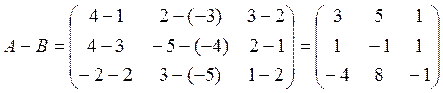Произведение матрицы A на число α=-3 есть матрица

.

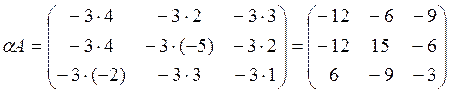Пример 2. Найти произведения матриц AB и BA, если они существуют:

1) , ;

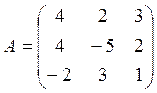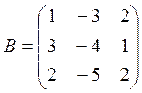2)  , .

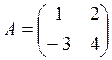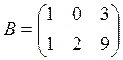Решение.

1) Матрица A  согласована с матрицей B, тогда, используя определение произведения матриц, находим

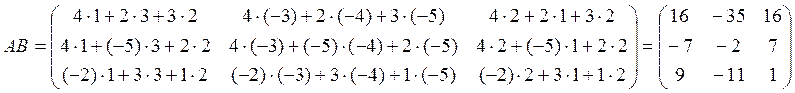 Матрица B  согласована с матрицей A, следовательно существует