Магнитный поток. Работа силы Ампера. Контур с током в магнитном поле. Энергия магнитного поля: Учебно-методическое обеспечение практического занятия

3.7. Магнитный поток.  Работа силы Ампера. 
Контур с током в магнитном поле.
Энергия магнитного поля  (2 часа)

3.7.1. Учебная цель занятия

Научить студентов применять следующие понятия и законы: Магнитный поток. Работа силы Ампера. Контур с током в магнитном поле.

3.7.2. Методические указания к проведению
занятия

Найти магнитный поток однородного и неоднородного магнитных полей.

Показать способы нахождения работы сил магнитного поля (сил Ампера) при различной ориентации контура с током в магнитном поле, энергии и плотности энергии магнитного поля, возникающего в соленоиде, при пропускании тока.

3.7.3. Рекомендуемая литература

[3] 5.4, 5.5, 5.9, 5.10;  [7] §3.

3.7.4. ПРИМЕРЫ  РЕШЕНИЯ  ЗАДАЧ

Пример 1. Вблизи бесконечного прямого провода расположена прямоугольная проволочная рамка со сторонами  мм и  мм. Рамка лежит в одной плоскости с проводом, причем стороны рамки длиной  мм параллельны проводу и ближайшая из них отстоит от провода на расстоянии  мм. Найти магнитный поток через рамку, если по бесконечному проводу течет ток силой  А.

Следовательно, определяя магнитный поток через рамку, необходимо проводить интегрирование по всей площади рамки. Для интегрирования разобьем поверхность рамки на узкие полоски длиной  и шириной  (рис. 1.1). Площадь полоски . В пределах такой полоски поле можно считать однородным. Элементарный поток вектора  через площадь  

      ,

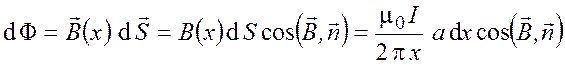где  – вектор единичной нормали к поверхности.

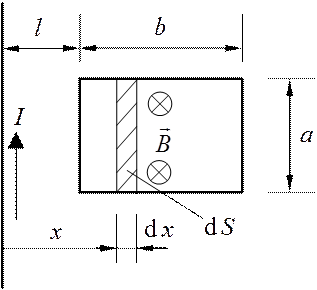Рис. 1.1

Магнитные силовые линии прямого тока – окружности, поэтому в любой точке плоскости рамки вектор  будет перпендикулярен плоскости рамки и .

Полный поток через поверхность рамки

                         .

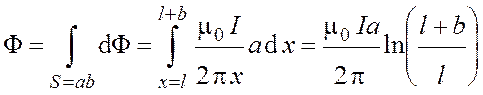Произведем вычисления:

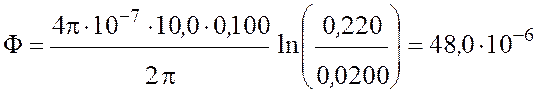      Вб.

Ответ:  Вб.

Пример 2. В однородном магнитном поле, индукция которого равна  мТл, находится плоская катушка радиусом  мм, содержащая  витков. Плоскость катушки составляет угол  с направлением вектора индукции. По виткам течет ток силой  А. Какую работу надо совершить, чтобы удалить катушку из магнитного поля? Сила тока в катушке все время остается неизменной.

Работа внешней, например механической, силы при перемещении катушки

                            .

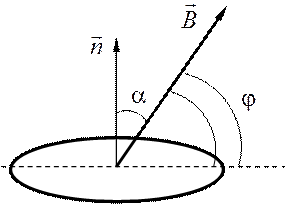Рис. 2.1

Потокосцепление (полный поток) в начальном положении катушки

               .

Потокосцепление в конечном положении катушки

                                , так как .

Таким образом,

                         .

Произведем вычисления:

 Дж.

Ответ:  Дж.

Пример 3 Соленоид с железным сердечником длиной  см и площадью поперечного сечения  см² содержит  витков. По обмотке протекает ток силой  А. Магнитная проницаемость железа составляет . Определить энергию и объемную плотность энергии магнитного поля соленоида.

Индуктивность соленоида

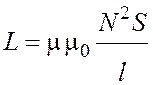                                        .                                        (3.2)

Подставим формулу (3.2) в выражение (3.1), получим

                                     .

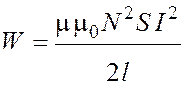Объемная плотность энергии

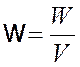                                              .                                              (3.3)

Объем соленоида

                                              .                                               (3.4)

Подставим формулу (3.4) в выражение (3.3), получим

                                              .

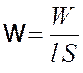Произведем вычисления

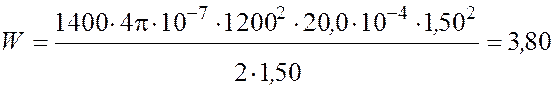    Дж;

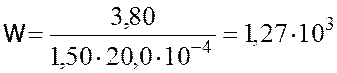                    Дж/м³.

Ответ:  Дж/м³.

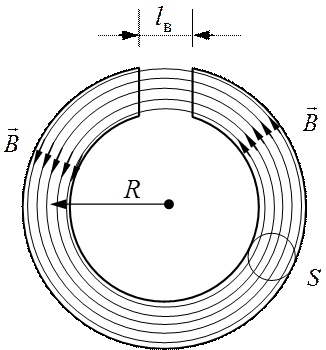
Пример 4. Средний радиус кольцевого (тороидального) железного сердечника  мм. В сердечнике имеется поперечный разрез длиной  мм (рис. 4.1). На сердечник намотан провод, по которому течет ток. Во сколько раз уменьшится индукция магнитного поля в воздушном зазоре сердечника, если немного разогнуть кольцо и увеличить длину зазора до  мм? Считать, что магнитная проницаемость железа остается неизменной и составляет . Рассеянием магнитного поля в воздушном зазоре пренебречь, ток обмотки не изменяется.

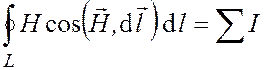                              ;                               (4.1)

Рис. 4.1

Считая, что силовые линии вследствие симметричности тороидальной катушки имеют форму окружностей, концентричных самому тору, проведем контур интегрирования  по средней линии тороида. Выберем направление обхода контура  так, чтобы оно совпадало с направлением силовых линий и тогда во всех точках интегрирования

                           и        .

Левая часть выражения (37.1)

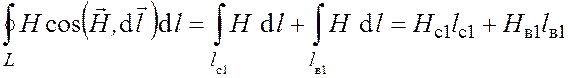     ,       4.2)

где  – напряженность магнитного поля на средней линии сердечника;  – напряженность магнитного поля на средней линии воздушного зазора;  – длина средней линии сердечника;  – длина средней линии воздушного зазора. Причем,

                                        .                                        (4.3)

Правая часть выражения (4.1)

                                           .                                           (4.4)

Таким образом, подставляя выражения (4.2) и (4.4) в формулу (4.1), получим

                                  .                                  (4.5)

Индукция связана с напряженностью:

                   ;            .                   (4.6)

Подставим выражения (4.6) и (4.2) в формулу (4.5), получим

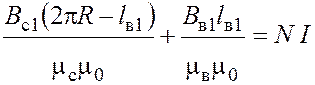                          .                           (4.7)

Так как магнитные силовые линии непрерывны, то значения магнитного потока внутри сердечника и внутри зазора одинаковые:

                         ;          .

По условию рассеянием магнитного поля в воздушном зазоре пренебрегаем, т. е. , поэтому

                                            .                                            (4.8)

Из выражения (4.7) с учетом формулы (4.8) получаем индукцию магнитного поля в воздушном зазоре:

                               .

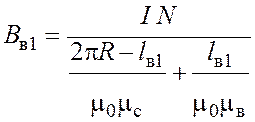Для случая с другим воздушным зазором  аналогично получим