











Научить студентов применять следующие понятия и законы: Внешний фотоэлектрический эффект. Квантовая теория внешнего фотоэффекта. Фотоны. Энергия, импульс, масса и скорость фотона. Эффект Комптона. Волны де Бройля.
При решении задач по данному разделу подчеркнуть, что все закономерности
фотоэффекта легко объясняются если, как предположил Эйнштейн, свет поглощается
и распространяется такими же порциями ![]() (квантами),
какими он, по предположению Планка, испускается. Привести формулу Эйнштейна для
внешнего фотоэффекта, ввести понятие задерживающего напряжения
(квантами),
какими он, по предположению Планка, испускается. Привести формулу Эйнштейна для
внешнего фотоэффекта, ввести понятие задерживающего напряжения ![]() и красной границы фотоэффекта.
Подчеркнуть, что в результате углубления представлений о свете выясняется его
двойственная природа. Интерференция, дифракция свидетельствуют о волновой
природе света, а фотоэффект, давление света и эффект Комптона подтверждают его
корпускулярную природу.
и красной границы фотоэффекта.
Подчеркнуть, что в результате углубления представлений о свете выясняется его
двойственная природа. Интерференция, дифракция свидетельствуют о волновой
природе света, а фотоэффект, давление света и эффект Комптона подтверждают его
корпускулярную природу.
[4] , Т.4, гл. 2; [8] стр. 4-8.
Пример 1. Определить максимальную скорость
фотоэлектронов, вырываемых с поверхности серебра: 1) ультрафиолетовым
излучением с длиной волны 155 нм; 2) ![]() -излучением
с длиной волны 1,00 пм.
-излучением
с длиной волны 1,00 пм.
|
Дано: |
Решение |
|
|
Максимальную скорость фотоэлектронов можно определить из уравнения Эйнштейна для фотоэффекта:
где |
![]() – работа выхода электрона из металла;
– работа выхода электрона из металла;
![]() – максимальная кинетическая энергия
вылетевшего фотоэлектрона.
– максимальная кинетическая энергия
вылетевшего фотоэлектрона.
Энергия фотона вычисляется по формуле
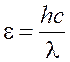 , (1.2)
, (1.2)
где ![]() – постоянная Планка;
– постоянная Планка; ![]() – скорость света в вакууме;
– скорость света в вакууме; ![]() – длина волны падающего излучения.
– длина волны падающего излучения.
Кинетическая энергия фотоэлектрона в зависимости от величины
скорости ![]() может быть выражена или по нерелятивистской
формуле
может быть выражена или по нерелятивистской
формуле
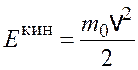 , (1.3)
, (1.3)
или по релятивистской формуле
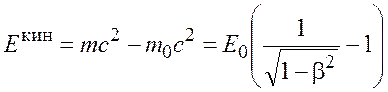 , (1.4)
, (1.4)
где ![]() – масса движущегося
электрона;
– масса движущегося
электрона; ![]() – масса покоя;
– масса покоя; ![]() – энергия покоя;
– энергия покоя; 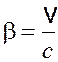 .
.
Если кинетическая энергия электрона много меньше его энергии
покоя ![]() , то применяется формула (1.3). Если же она
сравнима по величине с
, то применяется формула (1.3). Если же она
сравнима по величине с ![]() , то вычисление скорости по
формуле (1.3) приводит к ошибке, поэтому нужно пользоваться формулой (1.4).
Критерием выбора формулы служит погрешность, с которой необходимо рассчитать
скорость: если погрешность скорости должна быть не более 1 %, то при
соотношении энергий
, то вычисление скорости по
формуле (1.3) приводит к ошибке, поэтому нужно пользоваться формулой (1.4).
Критерием выбора формулы служит погрешность, с которой необходимо рассчитать
скорость: если погрешность скорости должна быть не более 1 %, то при
соотношении энергий ![]() можно использовать формулу
(1.3).
можно использовать формулу
(1.3).
1. Вычислим энергию фотона ультрафиолетового излучения по формуле (1.2):
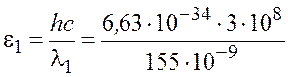 Дж
Дж![]() Дж;
Дж;
во внесистемных единицах
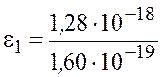 эВ
эВ![]() ,00 эВ.
,00 эВ.
Максимальная кинетическая энергия фотоэлектрона в первом случае
![]() .
.
Эта величина много меньше энергии покоя электрона (![]() МэВ). Следовательно, для данного
случая кинетическая энергия фотоэлектрона в формуле (1.1) может быть выражена
по нерелятивистской формуле (1.3). Таким образом,
МэВ). Следовательно, для данного
случая кинетическая энергия фотоэлектрона в формуле (1.1) может быть выражена
по нерелятивистской формуле (1.3). Таким образом,
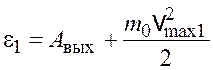 ,
,
откуда максимальная скорость фотоэлектронов
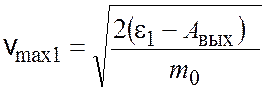 . (1.5)
. (1.5)
Подставив значения величин в формулу (8.5), найдем
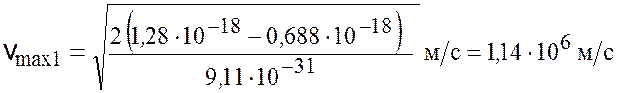 .
.
2. Вычислим энергию фотона ![]() -излучения:
-излучения:
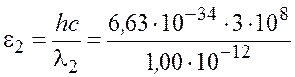 Дж
Дж ![]() Дж;
Дж;
во внесистемных единицах
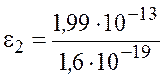 эВ
эВ![]() эВ
эВ![]() МэВ.
МэВ.
Максимальная кинетическая энергия фотоэлектрона во втором случае
![]() .
.
Эта величина больше энергии покоя электрона (![]() МэВ). Следовательно, для данного
случая кинетическая энергия фотоэлектрона в формуле (1.1) должна быть выражена
по релятивистской формуле (1.4):
МэВ). Следовательно, для данного
случая кинетическая энергия фотоэлектрона в формуле (1.1) должна быть выражена
по релятивистской формуле (1.4):
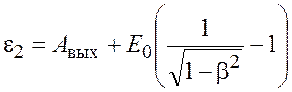 . (1.6)
. (1.6)
В нашем случае работа выхода много меньше энергии фотона ![]() -излучения, поэтому в формуле (1.6) работу
выхода учитывать не будем и получим
-излучения, поэтому в формуле (1.6) работу
выхода учитывать не будем и получим
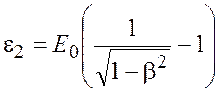 ;
;
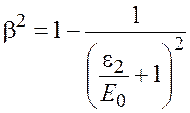 ,
,
откуда максимальная скорость фотоэлектронов
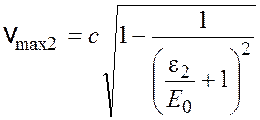 .
.
Произведем вычисления (энергии ![]() и
и ![]() входят в формулу в виде отношения, поэтому
их можно не выражать в единицах СИ):
входят в формулу в виде отношения, поэтому
их можно не выражать в единицах СИ):
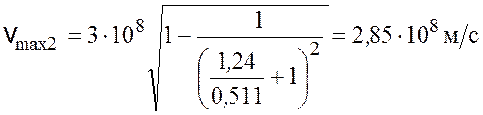 .
.
Ответ: ![]() ;
; ![]() .
.
Пример 2. Фотоэлектроны, вырываемые с поверхности серебра, задерживаются тормозящим электрическим полем при разности потенциалов 3,70 В. Определить длину волны излучения.
|
Дано: |
Решение |
|
|
Запишем уравнение Эйнштейна для фотоэффекта:
|
где ![]() – энергия фотона, падающего
на поверхность металла;
– энергия фотона, падающего
на поверхность металла;
![]() – работа выхода электрона из металла;
– работа выхода электрона из металла;
![]() – максимальная кинетическая энергия
вылетевшего фотоэлектрона.
– максимальная кинетическая энергия
вылетевшего фотоэлектрона.
Поскольку вылетевшие с поверхности металла фотоэлектроны полностью задерживаются тормозящим электрическим полем, то изменение их кинетической энергии равно работе сил электрического поля:
![]() , (2.2)
, (2.2)
где ![]() – заряд электрона.
– заряд электрона.
Энергия фотона вычисляется по формуле
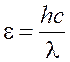 , (2.3)
, (2.3)
где ![]() – постоянная Планка;
– постоянная Планка; ![]() – скорость света в вакууме;
– скорость света в вакууме; ![]() – длина волны падающего излучения.
– длина волны падающего излучения.
Подставим выражения (2.2) и (2.3) в уравнение (2.1):
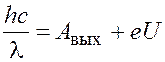 . (2.4)
. (2.4)
Тогда длина волны излучения
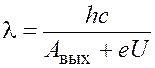 . (2.5)
. (2.5)
Подставив значения величин в формулу (9.5), найдем длину волны:
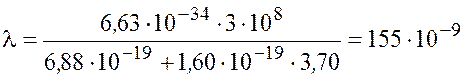 м = 155 нм.
м = 155 нм.
Ответ: ![]() нм.
нм.
Пример 3. В результате эффекта Комптона фотон был рассеян на свободном покоящемся электроне на угол 90°. Энергия рассеянного фотона 0,400 МэВ. Определить энергию фотона до рассеяния и кинетическую энергию электрона отдачи в электронвольтах.
|
Дано: |
Решение |
|
|
Энергия фотона
|
где ![]() – изменение длины волны фотона в
результате рассеяния на свободном электроне (
– изменение длины волны фотона в
результате рассеяния на свободном электроне (![]() и
и ![]() – длины волн фотона соответственно до и
после рассеяния);
– длины волн фотона соответственно до и
после рассеяния); ![]() – постоянная Планка;
– постоянная Планка; ![]() – масса покоя электрона;
– масса покоя электрона; ![]() – скорость света в вакууме;
– скорость света в вакууме; ![]() – угол рассеяния фотона.
– угол рассеяния фотона.
Энергия фотона связана с его длиной волны соотношением
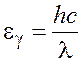 . (3.2)
. (3.2)
Формулу (10.1) с учетом (10.2) можно переписать в виде
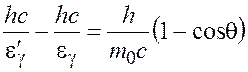 ,
,
откуда искомая величина энергии фотона до рассеяния
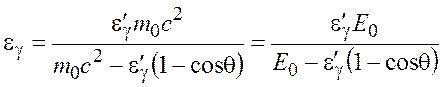 , (3.3)
, (3.3)
где ![]() МэВ – энергия покоя электрона.
МэВ – энергия покоя электрона.
Вычисления по формуле (10.3) удобнее вести во внесистемных единицах:
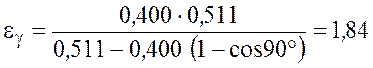 МэВ.
МэВ.
В соответствии с законом сохранения энергии в эффекте Комптона имеем
![]() ,
,
откуда кинетическая энергия электрона отдачи во внесистемных единицах
![]() МэВ.
МэВ.
Ответ: ![]() МэВ;
МэВ; ![]() МэВ.
МэВ.
Пример 4. В результате эффекта Комптона фотон с длиной волны 1,00 пм был рассеян на свободном покоящемся электроне на угол
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.