Лабораторная работа № 5
Исследование электрического сопротивления металлов
и полупроводников в области низких температур
Цель работы. Изучить температурную зависимость электрического сопротивления металлов и полупроводников в диапазоне температур (90 ... 300) К.
5.1. Исходные сведения.
В настоящей работе для измерения электрического сопротивления как функции температуры удается использовать имеющийся в лаборатории универсальный стенд. Стенд, как мы знаем, в основном предназначен для теплофизических исследований. Электронный аналого-цифровой контроллер стенда содержит 8 каналов измерения температуры. Однако каждый из них может использоваться не только по своему прямому назначению. Так, любой из первых четырех каналов, непосредственно использующихся для регистрации сигналов термопар, можно применять также для измерения электродвижущей силы (ЭДС) различных источников тока. В свою очередь, каналы 5–8, непосредственно предназначенные для измерения температуры медными термометрами сопротивления и микротермисторами, вполне пригодны для изучения электропроводности (а, следовательно, и удельного электрического сопротивления) разнообразных металлов и полупроводников. Ограничением для таких измерений могут служить лишь трудности изготовления образцов с заданными номинальными значениями электрического сопротивления. У каналов 5, 6 область номинальных значений сопротивления лежит в пределах 1 … 3 Ом, а у каналов 7, 8 –в пределах 0,5 … 20 кОм. Однако во многих случаях указанные ограничения удается преодолеть весьма простыми средствами. Для расширения рабочих диапазонов каналов можно включать в электрическую цепь исследуемого резистора дополнительные или шунтирующие сопротивления. Чтобы убедиться в этом, вспомним исходные сведения об электрических цепях постоянного тока.
Для измерений электрического сопротивления используется широко известный закон Ома, согласно которому в линейных однородных проводниках постоянного сечения S сила тока I всегда пропорциональна падению напряжения U на его рабочем участке длиной l и обратно пропорциональна электрическому сопротивлению R этого участка
,
,
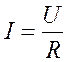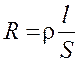(5.1.1)
где r – удельное электрическое сопротивление линейного проводника, непосредственно зависящее от его материала, температуры и физического состояния.
Замечание. Закон Ома внешне очень прост и отличается чрезвычайной универсальностью. В действительности же он имеет сложную квантовомеханическую природу и его простота иллюзорна. Анализ физической сущности закона Ома выходит за рамки данной работы.
Из выражений (5.1.1) следует, что для определения электрического сопротивления проводника необходимо одновременно измерять падение напряжения U и ток I на рабочем участке проводника. Поэтому опыты по измерению электрических сопротивлений обычно ставят так, чтобы один из параметров электрической цепи (U или I) оставался неизменным на протяжении всего процесса измерений. Каналы 5–8 в контроллере обеспечивают непосредственную регистрацию падения напряжения на проводнике, сохраняя в опытах строго заданное значение проходящего по нему тока.
Стабилизация тока в канале осуществляется достаточно простым способом. Чтобы понять его сущность, достаточно обратиться к рис. 5.1.1.
 |
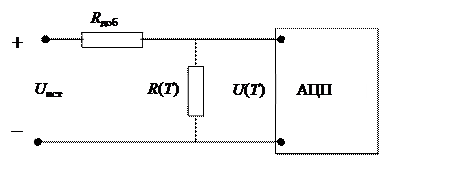Рис. 5.1.1. Схема измерения электрического сопротивления R(T).
Аналого-цифровой преобразователь (АЦП) контроллера регистрирует изменяющееся падение напряжения U(Т) на исследуемом резисторе R(T). Входное сопротивление АЦП не шунтирует R(T), так как на три порядка (в 1000 раз и более) превышает его величину. Поэтому для фиксации тока в электрической цепи следует использовать источник стабилизированного напряжения Uист и выполнять в опытах условие
Rдоп >>> R(T). (5.1.2)
Благодаря высокой чувствительности используемого АЦП оптимальными являются значения U » (1 … 10) мВ, поэтому условие (5.1.2) удается обеспечить при напряжении стабилизированного источника Uист » 20 В.
Это позволяет нам воспользоваться широкими техническими возможностями стенда и исследовать температурную зависимость электрического сопротивления проводников в условиях их поочередного плавного охлаждения или нагрева в соответствующих сосудах-термостатах стенда. Требуется лишь зарегистрировать в опыте температуру T(t) исследуемого проводника и падение напряжения U(t) на нем как функции времени t.
Рабочие расчетные формулы в данной лабораторной работе могут быть представлены в виде
,
, 
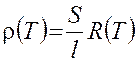, (5.1.3)
где A – коэффициент, обратный величине тока, проходящего через проводник ("постоянная" канала). Для его определения к каналу следует подключить эталонный резистор, сопротивление которого хорошо известно (аттестовано метрологическим учреждением). Коэффициент А канала в этом случае можно вычислить с помощью соотношения
.
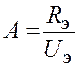(5.1.4)
Замечание. При градуировке канала часто возникает необходимость определения его нулевого напряжения U0, которое имеет место при коротком замыкании входных клемм канала. В общем случае отсчет напряжения U(t) должен производиться от нулевого напряжения U0 канала.
Падение напряжения UR на исследуемом сопротивлении R(Т) зависит от температуры образца и регистрируется с высокой точностью 16-ти разрядным аналого-цифровым преобразователем АЦП, который сохраняет в широком диапазоне изменения электрических сигналов чувствительность не менее 10 мкВ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
