Исследование процесса теплоотдачи в кипящем азоте (Лабораторная работа № 6)

Лабораторная  работа  № 6

Исследование процесса теплоотдачи в кипящем азоте

Цель работы. Изучение закономерностей конвективного теплообмена в кипящем жидком азоте и определение коэффициента теплоотдачи.

6.1. Исходные сведения

Известно, что в природе существуют три формы теплообмена:

– теплообмен на молекулярном уровне, посредством хаотичных, тепловых соударений микрочастиц вещества (теплопроводность);

– теплообмен посредством электромагнитного поля (излучение);

– теплообмен на макроскопическом уровне, посредством видимого пространственного перемещения вещественной среды (конвекция).

Теплопроводность наблюдается внутри любых веществ. Источниками электромагнитного излучения являются нагретые тела. Поэтому теплообмен излучением наиболее ярко проявляется в вакууме и в слабо селективных прозрачных средах, разделяющих нагретые тела. Конвективная форма теплообмена наблюдается только в жидких и газообразных средах. Она может возникать самостоятельно, когда в среде возникает тепловая неоднородность, и начинают проявляться силы Архимеда (гравитационная, естественная конвекция). Но может создаваться и принудительно (вынужденная конвекция), под влиянием внешних факторов (ветер, вентиляторы, насосы и др.).

В жидкостях перенос тепла обычно осуществляется одновременно конвекцией и теплопроводностью. При этом наличие конвекции наиболее ощутимо проявляется на границе теплообмена твердой стенки с жидкостью или газом. Такой теплообмен, ввиду его специфичности, получил самостоятельное название. Его принято называть конвективной теплоотдачей или просто теплоотдачей. Процесс теплоотдачи зависит от множества внешних факторов и отличается повышенной неустойчивостью. Различают ламинарную и турбулентную теплоотдачу. Закономерности последней наиболее сложны, поэтому их обычно изучают по возможности в натурных условиях.

Еще И. Ньютон и Г. В. Рихман, изучая в XVIII веке теплообмен твердых тел в открытой воздушной среде, независимо друг от друга пришли к выводу, что количество тепла, отдаваемое (или воспринимаемое) телом, прямо пропорционально разности температур между поверхностью и окружающей средой. Этот опытный факт, справедливый при малых разностях температур между поверхностью тела  и окружающей средой , обычно называют законом теплоотдачи Ньютона и аналитически представляют в виде

,                                  (6.1.1)

где  – тепловой поток, Вт;  – коэффициент теплоотдачи, Вт/(м²·град);  – поверхность теплообмена, м².

Коэффициент теплоотдачи существенно зависит от участка на поверхности тела, помещенного в среду, поэтому в уравнение (6.1.1) входит интегральный, усредненный по всей поверхности тела коэффициент теплоотдачи. Локальный коэффициент теплоотдачи на участке dF поверхности тела следует определять с помощью выражения

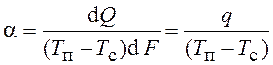,      Вт/(м²·град).                (6.1.2)

Коэффициент теплоотдачи  является не только функцией формы и размеров тела, но также зависит от режима движения и температуры жидкости, от ее физических свойств, гравитационного поля и ряда других внешних факторов. Рассчитать его аналитически чаще всего не удается. Поэтому коэффициент теплоотдачи в реальных изделиях практически всегда определяют экспериментальным путем. Для его определения обычно используются стационарные методы и несколько реже методы регулярного теплового режима.

Жидкий азот широко применяется в системах глубокого охлаждения, причем практически всегда в режиме кипения. Жидкий азот обычно принудительно прогоняют по трубам теплообменника. Закономерности теплоотдачи в таких системах принято исследовать стационарными методами, измеряя интенсивность испарения азота. Однако при лабораторных исследованиях для быстрого охлаждения небольших по размеру объектов их часто помещают непосредственно в ванну с жидким азотом. В этом случае для количественной оценки коэффициента теплоотдачи в азоте наиболее удобным и простым в реализации оказывается метод регулярного режима.

Метод регулярного теплового режима обычно применяется при исследовании интегральных коэффициентов теплоотдачи тел сложной формы. Интенсивность теплоотдачи не зависит от материала тела, поэтому при ее исследовании тело интересующей формы, как правило, изготавливают из металла с известной удельной теплоемкостью, придают ему заданную форму и используют одновременно в качестве энтальпийного тепломера (a-калориметра). Такой калориметр предварительно нагревается или охлаждается относительно исследуемой конвективной среды и погружается в нее. Температура калориметра регистрируется термопарой, "холодный" спай которой располагается непосредственно в исследуемой среде, на значительном удалении от калориметра. Интегральный тепловой поток, которым обменивается калориметр со средой, оказывается однозначно связанным со скоростью изменения его температуры. Согласно тепловому балансу между телом и конвективной средой, для расчета интегрального коэффициента теплоотдачи между ними справедливо выражение

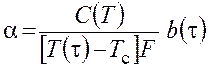,                                   (6.1.3)

где  – температура тела-калориметра как функция времени; C(T) – теплоемкость тела как функция температуры; F – поверхность тела; 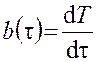 – скорость изменения температуры тела (функция времени).

6.2. Содержание и основные этапы работы.