Решение многомерных линейных задач теплопроводности.
Температурное поле рассматриваемой заготовки описывается с помощью линейного двумерного уравнения теплопроводности
|
|
c граничными условиями первого рода в плоскостях симметрии и третьего рода на поверхности.
Для решения предложенной задачи были реализованы в виде программы различные методы математического моделирования [1, 2]. Выявлены характерные критерии оценки рассматриваемых методов с точки зрения их сходимости, устойчивости, близости получаемых решений к аналитическому.
Проведенное расчетное исследование показало, что наилучшие результаты дает метод расщепления, сочетающий в себе высокую точность полученных результатов, по отношению к аналитическому решению (рис. 1), малое время работы и небольшой объем занимаемой оперативной памяти (Таблица 1).
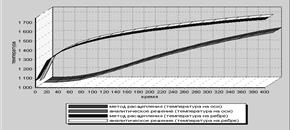
Рис 1. Решение уравнения теплопроводности аналитическим методом и методом расщепления.
Таблица 1. Показатели эффективности, полученные при программной реализации различных методов решения многомерной линейной задачи теплопроводности.
|
Методы |
Машинное время, с |
Оператив. память, Кб |
|
метод простой итерации |
1,56 |
8,854 |
|
метод итерации Гаусса-Зейделя |
1,638 |
1,85 |
|
метод расщепления |
1,275 |
7,564 |
|
метод переменных направлений |
1,28 |
7,896 |
|
метод Гаусса |
1,215 |
26,35 |
Решение многомерных нелинейных задач теплопроводности.
В случае введение температурной зависимости теплопроводности l и теплоемкости с основное уравнение теплопроводности (1) становится нелинейным относительно температуры и выглядит следующим образом:
|
|
(2) |
Данная постановка нелинейной задачи предполагает сведение ее к линейной в случае явной зависимости l = l(Т). Линеаризация проводилась с помощью прямого и итерационного методов. Прямой метод оказался эффективным для небольшой зависимости теплопроводности от температуры. Итерационный метод, напротив, показал наилучшие результаты в случае резкой температурной зависимости теплофизических характеристик, поскольку линеаризация, в рамках данного подхода, выполняется на каждом временном интервале.
Нелинейность граничных условий, является результатом излучения на поверхности металла. Применение метода конечных разностей приводит к системе уравнений, где лишь одно из балансовых уравнений является нелинейным. Его решение проводится с помощью итерационных методов [1,2]. Наилучшие результаты показал метод Ньютона, который имеет более высокую сходимость и лучше ведет себя в широком температурном и временном диапазоне. Количество итераций, требуемых для метода Ньютона существенно меньше, чем для других методов.
Таким образом, в данной работе разработан программный модуль, с помощью которого было проведено решение задач многомерной теплопроводности на основе традиционных методов математического моделирования и осуществлен сравнительный анализ показателей эффективности этих методов на примере двумерной задачи.
Задача теплопроводности:распределение температуры внутри тела
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.