Исследование процесса локального разрушающего криовоздействия на биологический объект: Методические указания к лабораторным работам по курсу «Криогенные технологии в медицине и биологии», страница 2

Рис. 1. Тепловая схема разрушающего криовоздействия на биологический объект.

Биологический объект представляет  собой структуру, состоящую из здорового органа 1 и новообразования 2. Размеры органа значительно превышают размеры новообразования: >>_, поэтому температура объекта на его внутренней, пассивной, границе постоянна  . Новообразование представляется в виде сферического включения с радиусом , расположенного на поверхности органа  1.

Тепловая задача локального разрушающего криовоздействия состоит в переохлаждении новообразования     1    от начальной температуры     , до температуры гарантированного криоповреждения (некроза)  К.

Геометрически, разрушающее криовоздействие можно считать законченным в тот момент, когда изотерма . находится за пределами новообразования 1. Известно, что биологические ткани частично повреждаются при температурах ниже 270 К, соответственно в объекте локального разрушающего воздействия формируется зона частичного криоповреждения, ограниченная изотермическими сферами  и .

Криоповреждение здоровой части органа является негативным побочным эффектом криохирургического вмешательства, поэтому при разработке технологии локального разрушающего криовоздействия необходимо добиваться снижения объема области повреждения   →.

Поиск технологических приемов, обеспечивающих минимальный объем криотравмы, является одной из учебных целей лабораторной работы.

Учитывая известные из практики сведения о размерах новообразований, принимаем =50 мм.

Таблица  1

Теплофизические свойства покровных тканей человека

Для формирования условий однозначности вычислительного эксперимента принимаем начальную температуру объекта равной температуре внутренних органов человека ^oC.                                      

2. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОБЪЕКТА ЛОКАЛЬНОГО ОХЛАЖДЕНИЯ

Для описания переноса теплоты через слои охлаждаемых биологических  объектов обычно используется уравнение энергии в одномерном виде [4]:

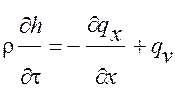                                                ,                                                    (1)

где   h – энтальпия (теплосодержание) материала, образующего слой, q_х – тепловой поток вдоль координаты х, q_v –теплота, выделяемая внутренними источниками в единице объема.

С учетом специфики процесса охлаждения и допущений, принятых при построении физической модели рациональнее использовать запись уравнения энергии в сферических координатах:

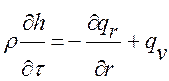                                            (1а)

При замене в уравнении (1а) производных конечно–разностными приближениями [2] получено:

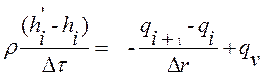                                    ,                      (2)

где  h^′_i  –энтальпия в  ί-точке в момент времени τ+∆τ, q_i, q_i+1 – соответственно подвод теплоты от соседних сферических объектов.

Решая  уравнение (2) относительно h^′_i  , получаем: 

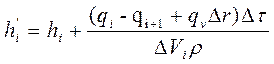                                     .                        (3)

Перенос теплоты  вдоль оси через полусферическую границу элементарного участка   определяется  выражением :

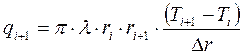                                                                                       (4)

Для всех элементарных полусфер при <1 тепловой поток от предыдущей сферы определен при расчетах теплового баланса предыдущего участка (см. рис. 2)

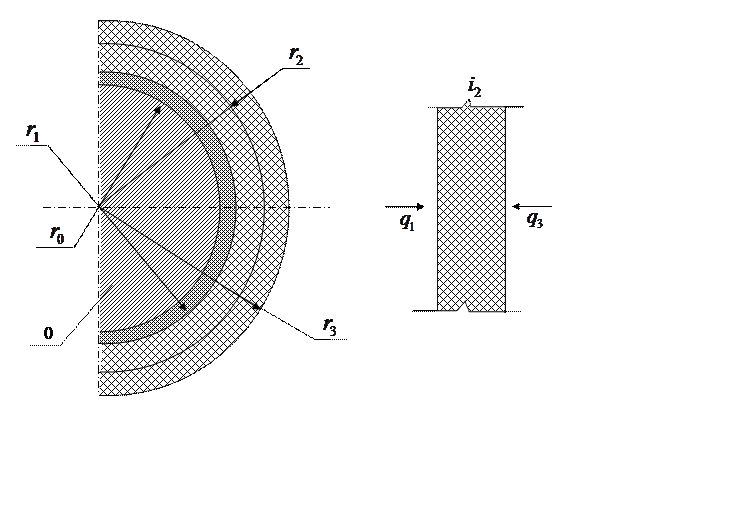
Рис. 2  Тепловая схема процесса разрушающего криовоздействия на биологический объект

Так для полусферы  теплоприток со стороны полусферы определяется как:

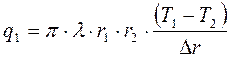                                              .                                          (5)

Это выражение уже использовалось при определении теплового потока  при :

                                            .                                          (6)

Формулы 5 и 6 идентичны и различаются только знаком, который имеет тепловой поток. С учетом этого для всех участков с >1 значение  не вычисляется, а учитывается ранее полученный результат. В общем случае для учета значения  используется буферная переменная – тепловой поток от предыдущего участка . Для каждого участка кроме =1 тепловой баланс записывается в виде: