Моделирование нестационарного теплообмена при охлаждении оболочки тела жидким или газообразным теплоносителем: Методические указания к лабораторным работам по курсу «Криогенные технологии в медицине и биологии», страница 4

                                                       (14)

Для расчета значений Nu и α используются комплексные формулы, сформулированные при выполнении лабораторной работы №1.

Ввод стандартных данных

Формирование листа «Гипотермия» начинается с ввода таблицы, характеризующей свойства покровообразующих слоев (см. рис. 4).    Кроме того вводятся сведения о толщине покровных слоев, высоте объекта охлаждения и параметрах сетки разбиения (∆τ и ∆x).

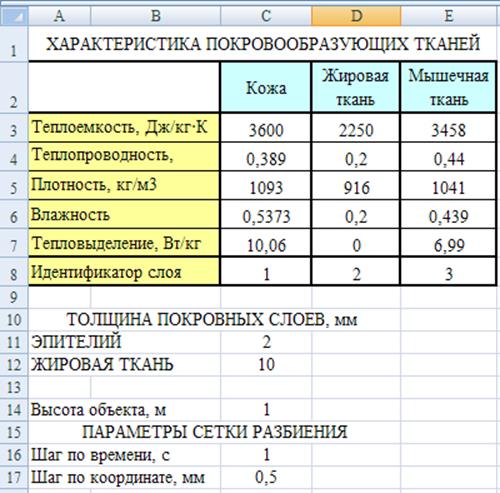
Рис. 4. Ввод характеристик покровных слоев, параметров объекта

 и сетки разбиения

Затем создается матрица характеристик узловых точек. Матрица содержит сведения о значениях х_i, ns_i, c_i, λ_i, ρ_i, φ_i, q_i (см. рис. 5).

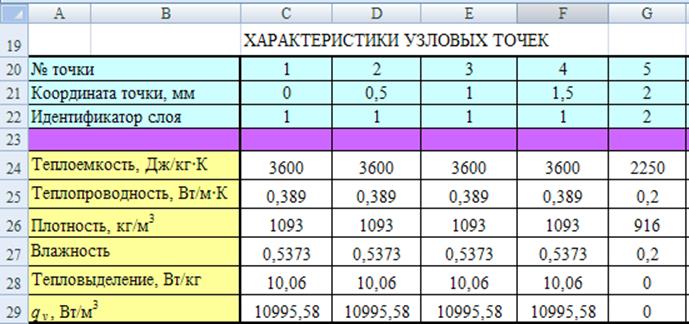
Рис. 5. Характеристики узловых точек математической модели объекта охлаждения

Данные массива формируются автоматически на основе данных о толщине слоев и шаге по координате ∆x. Сначала вычисляется значение x_i для каждой точки (см. рис. 6).

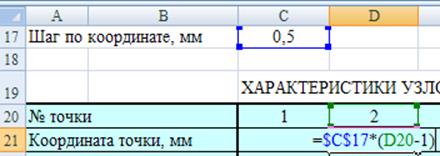
Рис. 6.  Вычисление координаты узловой точки

Затем по известной координате x_i и толщине слоев δ_э  и  δ_ж для каждой точки вычисляется значение идентификатора ns_i (см. рис. 7). Для этого используется двойная функция «ЕСЛИ». Логический оператор сравнивает текущую координату x_i с толщиной слоев и присваивает точке соответствующий идентификатор. Изменение исходной толщины слоев вызывает изменение матрицы ns_i. На основании значения идентификатора ns_i  заполняются ячейки, содержащие характеристики точки.

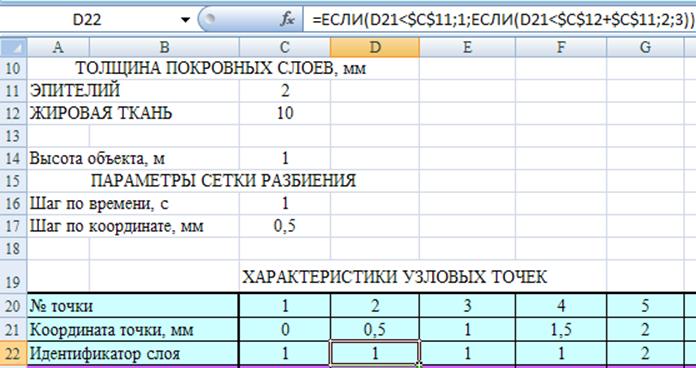
Рис. 7. Определение идентификатора узловой точки

Далее вычисляются теплофизические свойства слоев для всех узловых точек посредством функции «ЕСЛИ», которые считываются из таблицы с характеристиками слоев (см. рис. 8).

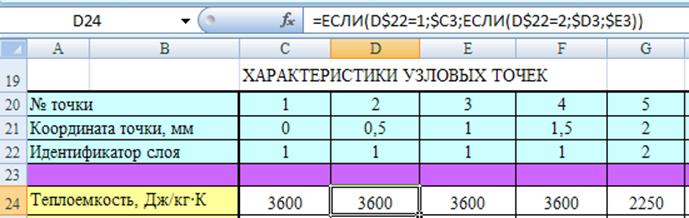
Рис. 8. Выбор значения теплоемкости по значению идентификатора точки

Проведение эксперимента предполагает контроль температуры на внешней и внутренней границах жирового слоя T_i = n₁ и T_i = n₂. Значения n₁ и n₂ определяем с помощью поиска позиции: «ПОИСКПОЗ». Оператор просматривает матрицу ns_i и возвращает адрес первой ячейки, содержимое  которой равно 2 или 3 (см. рис. 9).

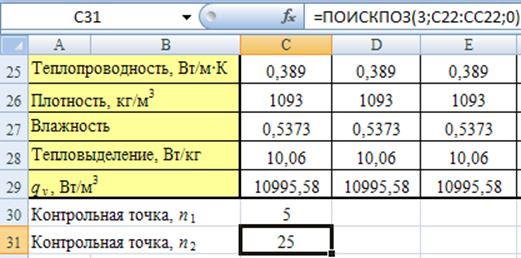
Рис. 9. Определение номера точки контроля температуры n₂

Затем производится ввод условий однозначности. Задаются граничные и начальные условия эксперимента (см. рис. 10).

Рис. 10. Ввод условий однозначности численного эксперимента

На основании начальных условий определяется температура и энтальпия узловых точек в момент (см. рис. 11). Для вычисления температур используется функция «ЕСЛИ».

Далее следует сформировать алгоритм расчета изменения энтальпии узловых точек во времени.

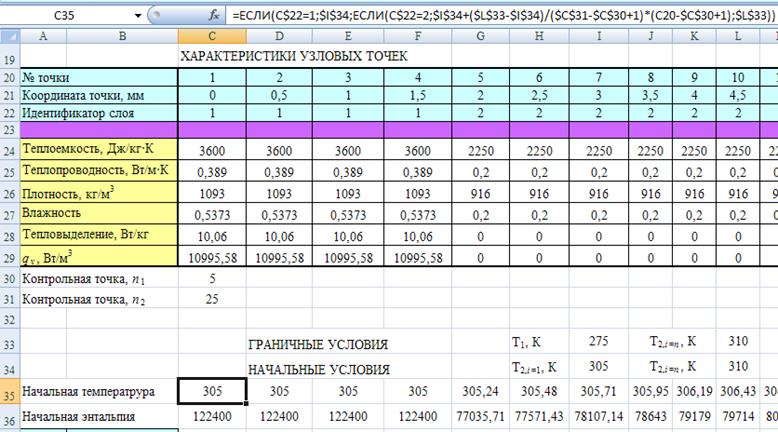
Рис. 11. Определение начальных значений температуры и энтальпии узловых точек

Вычисление изменения энтальпии

Изменение энтальпии узловых точек происходит под действием внешнего конвективного отвода теплоты:

.

Температура теплоносителя Т₁ и поверхности объекта охлаждения  Т₂ определены  (см. рис. 11), поэтому для расчета конвективного отвода теплоты необходимо определить коэффициент теплоотдачи α:

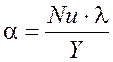
 Порядок построения комплексной формулы изучен в рамках лабораторной работы №1. Формулы для вычисления критериев Прандтля и Релея обращаются к листу «Свойства воды» для получения данных о физических характеристиках теплоносителя (см. рис. 12, рис. 13).

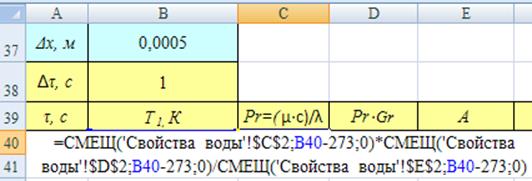
Рис. 12. Вычисление критерий Прандтля

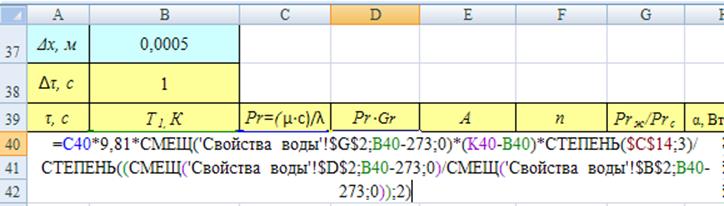
Рис. 13. Вычисление критерия Релея

Для расчета коэффициентов A и nможно воспользоваться рекомендациями лабораторной работы №1. В конечном итоге коэффициент теплоотдачи определяется формулой, приведенной на рис. 14.

Рис. 14.  Комплексная формула для расчета коэффициента теплоотдачи

при естественной конвекции воды

Далее, для удобства вычислений и обработки результатов эксперимента, в первом столбце матрицы вычислений формируются значения             τ_i+1= τ_i +∆τ, где 0 < τ_i  < 300 с. Вычисление элементов теплового баланса элементарной точки организовано в трех последовательных ячейках Т_i , h_iи q_i+1.

На первом временном слое значения Т_i и h_iсчитываются из массивов «Начальная температура» и «Начальная энтальпия» (см. рис. 15).

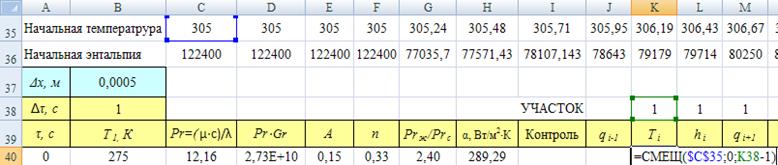
Рис. 15. Определение температуры узловой точки

на первом временном слое

Для последней узловой точки задается значение температуры, которое определяется в соответствии с граничными условиями эксперимента (см. рис. 16).

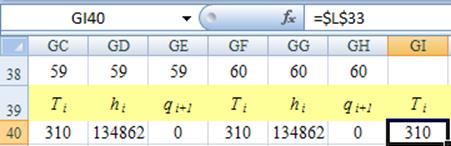
Рис. 16. Определение температуры на пассивной границе

моделируемого объекта

Для первой узловой точки выполняется вычисление                        q_i-1= α∙(T₂ - T₁) (см. рис. 17).