Моделирование нестационарного теплообмена при охлаждении оболочки тела жидким или газообразным теплоносителем: Методические указания к лабораторным работам по курсу «Криогенные технологии в медицине и биологии», страница 2

 

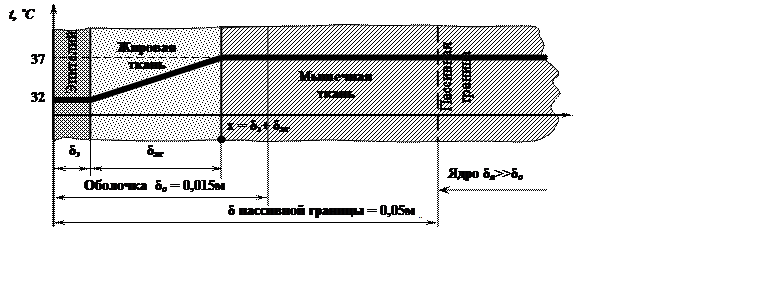
Рис. 1. Тепловая схема объекта охлаждения

В нормальных условиях через оболочку проходит тепловой поток от ядра тела q_я ≈ 100 Вт/м², поэтому температура поверхности тела выше температуры ядра: t_о > t_я.

Температура ядра постоянна: t_я = 37 ºС. Температура наружной поверхности зависит от интенсивности конвективного отвода теплоты в окружающую среду, обычно t_о  = 32 ºС.

Начальное распределение температуры покровных слоев принято по данным, известным из литературы  [6]. 

Таблица  1

Теплофизические свойства покровных тканей человека

Орган    или ткань	Плотность, кг/м3	Содержание воды, %	Теплоёмкость, Дж/кг·К	Теплопроводность, Вт/м·К	Тепловыделение, Вт/кг
Эпителий	1093	53,5 –72,5	3600	0,389	10,06
Мышцы	1041	68,5– 80,3	458	0,439	6,99
Жировая ткань	916	15 – 20	250	0,200	–

2. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОБЪЕКТА ОХЛАЖДЕНИЯ

Для описания переноса теплоты через слои охлажденного объекта используем уравнение энергии в одномерном виде 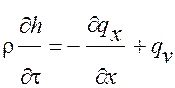[1]:

                                                ,                                                    (1)

где   h – энтальпия (теплосодержание) материала, образующего слой, q_х – тепловой поток вдоль координаты х, q_v –теплота, выделяемая внутренними источниками в единице объема.

При замене в уравнении (1) производных конечно–разностными приближениями получено:

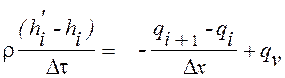                                   ,                    (2)

где  h^′_i  –энтальпия в  ί-точке в момент времени τ+∆τ, q_i, q_i+1 – соответственно подвод теплоты от узловых точек.

Решая  уравнение (2) относительно h^′_i  , получаем: 

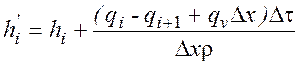                                   .                      (3)

Эта схема аппроксимирует исходную задачу с первым порядком погрешности О(∆х+∆τ) и является условно устойчивой (следовательно, сходящейся) при числе Фурье:

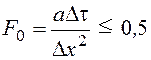                                                             ,                                 (4)

где  а=λ/cρ – коэффициент температуропроводности.        

По известным теплофизическим характеристикам слоев объекта охлаждения (см. табл. 1) можно оценить допустимое значение шага по времени ∆τ (см. табл. 2).

                                                                  Таблица 2

Расчет величины шага по времени

Ткань	а, м2/c	∆τ, с
Эпителий	9,89·10-8	1,26
Жировая ткань	12,2·10-8	1,08
Мышца	9,7·10-8	1,29

Тогда, при Dx = 0,5ּ10^–3 м  выбираем ∆τ = 1 с.

Перенос теплоты  вдоль оси Х  определяется законом Фурье:

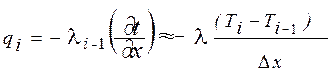                                  ,                               (5)

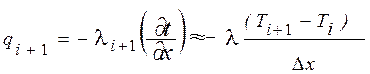                              ,                             (6)

где  Dx  – расстояние между точками (шаг разбиения).

Подвод теплоты от внутренних источников:                             

                                                       ,                                               (7)                         

            где  q_g – удельное тепловыделение ткани (см. табл. 1)

От наружной поверхности моделируемого объекта (при i = 1)  теплота отводится  посредством конвективного теплообмена:

                                               ,    (8)

где  α  – коэффициент теплоотдачи; T₁ – температура  теплоотводящей среды.

Выражение (8) представляет собой граничное условие третьего рода, определяющее взаимодействие моделируемого объекта с газообразным теплоносителем.

На пассивной границе объекта используем условия первого рода t_я = const = 37,0 ˚С.

Начальные условия для объекта охлаждения задают распределение температуры в слоях при .

Общее число элементарных участков  в пределах пассивной границы принимает n = 100.

К числу возможных экспериментальных задач относится исследование влияния толщины покровных слоев, поэтому в модели предусмотрена возможность их варьирования. По  заданным толщинам  покровных  тканей:  δ_э − толщина эпителия,  δ_ж − толщина жировой ткани рассчитываются координаты границ: х₁ = δ_э и  х₂ = δ_э + δ_ж. Формируем целочисленный массив ns, который содержит индекс − признак моделируемого слоя:

если   1 ≤ х_i < х₁ , то ns = 2 (эпителий),

если  х₁ ≤ х_i < х₂ , то ns = 3 (жировая ткань),