Моделирование нестационарного теплообмена при охлаждении оболочки тела жидким или газообразным теплоносителем: Методические указания к лабораторным работам по курсу «Криогенные технологии в медицине и биологии», страница 3

если  х₂ ≤ х_i , то ns = 1 (мышца).

Вычисляются и фиксируются номера узловых точек, соответствующих границам слоев: n₁ и n₂.

Массив начальных значений температур  необходимо сформировать с учетом заданного геометрического строения объекта. Значения температуры в момент времени τ = 0:

если ns = 2,  то ,

если ns = 3,  то ,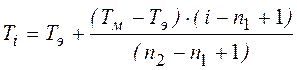

если ns = 1,  то .

Начальное теплосодержание для узловой точки вычисляется по начальному значению температуры:

                                            ,                                        (9)                

где Т^* − температура дефростации,  Т^*=271 К, с_nsi − удельная теплоемкость текущего слоя покровообразующих тканей.

Описанный алгоритм формирования начальных массивов температуры и энтальпии слоев выполняется в начале численного эксперимента τ = 0 . На всех последующих временных слоях τ > 0 энтальпия вычисляется  из уравнения энергии. Значения температуры рассчитываются по величине энтальпии    T_i^' =f ( h_i^' ).

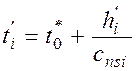                                                   .                                           (10)                

Для повышения точности и сокращения объема расчетов целесообразно составлять для каждого узла локальный тепловой баланс.

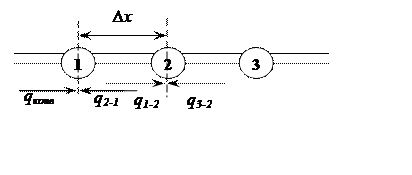      Рис. 2. Локальные тепловые балансы соседних узловых точек

Схема вычисления теплового баланса узловой точки (см. рис. 2) строится на основе представления о том, что тепловые потоки направлены в текущую узловую точку. Действительная физическая картина процесса переноса теплоты описывается знаком, который имеет вектор теплового потока. Если поток повышает теплосодержание точки, его знак положительный, и наоборот. Знак потока определяется из градиента температур.  Например, от последующей точки определяется выражением:

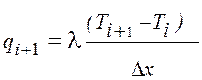                                        (11)

Соответственно при Т_i+1 > Т_i тепловой поток от последующей точки положительный q_i+1 >0.

Принцип построения локального теплового баланса поясняется рис.2. Для первой точки подвод теплоты от предыдущего участка определяется конвективным отводом теплоты: при i= 1 q_i-1 = q_конв, подвод теплоты от последующей точки  q_i+1 или q_2-1 определяется из (12):

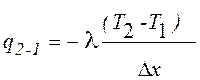                                                    .                                (12)

Из тепловой схемы (см. рис. 2) видно, что тепловой поток, подводимый от второго узла к первому q_2-1, равен по величине тепловому потоку, поступившему из первого узла ко второму q_1-2, но имеет другой знак: q_2-1 = -q_1-2. 

Это позволяет сократить объем вычислений и вероятность ошибок. Для учета результатов вычислений, выполненных для предыдущего узла, введем буферную переменную q_пред = -q_2-1, которая используется для описания количества теплоты, полученного от предыдущей точки. Тогда выражение (3) для всех точек примет вид:

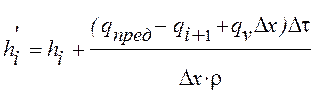                                                               (13)

Для первой узловой точки    подвод теплоты от предыдущего участка определяется конвективной теплоотдачей q_пред = q_конв. После вычисления величины h^′₁ для первой точки производится присвоение q_пред = -q_i+1, соответственно при переходе к вычислению энтальпии второй узловой точки величина  q_пред известна.

ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ

Лабораторная работа проводится в 2 этапа:

1. Разработка алгоритма вычисления.

2. Выполнение численного эксперимента по индивидуальным исходным данным.

Разработка алгоритма вычислений

Описанная выше математическая модель реализуется в виде электронной таблицы EXEL. Так как в работе необходимо рассмотреть процессы в условиях охлаждения жидким и газообразным теплоносителем, математическое моделирование выполняется на двух листах книги EXEL: «Гипотермия» и «Криотерапия».

Далее будет рассмотрен порядок подготовки расчетов на листе «Гипотермия».

База стандартных данных

Для определения физических свойств воды в численном эксперименте используется таблица EXСEL (см. рис. 3). Таблица размещается на отдельном листе «Свойства воды».

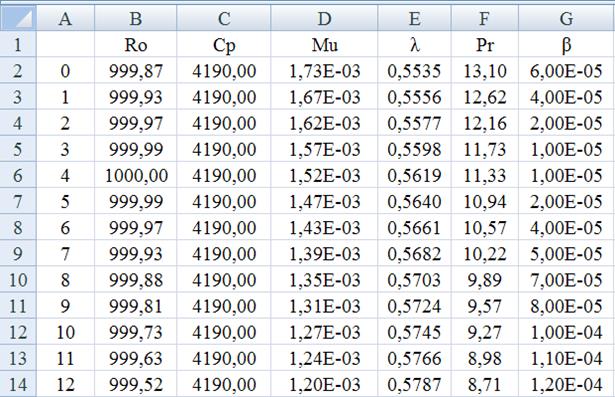
Рис. 3. Данные стандартных свойств воды в интервале температур от 0 до 36 ^оС

Данные листа «Свойства воды» используются для расчетов коэффициента теплоотдачи. В пределах интервала температур 0 ≤ t ≤ 36 ºC  число Прандтля для воды существенно изменяется: Pr₀ = 13,10,           Pr₃₆ = 4,73, отношение Pr_c / Pr_ж  всегда больше 1. Это необходимо учитывать при расчете критерия Нуссельта. Для жидкостей рекомендовано выражение: