Быстрое преобразование Фурье (Лабораторная работа № 2)

Лабораторная работа №2

Быстрое преобразование Фурье

Цель работы: Изучение Быстрого преобразования Фурье.

Необходимые теоретические сведения

Рассмотрим алгоритмы БПФ с основанием 2, которые применяются к последовательностям длины N=2^l, l – целое.

Основная идея БПФ состоит в следующем. Последовательность x[n] разбивают на две N/2 – точечные последовательности x₁[n] и х₂[n], и находят для них X₁[k] и X₂[k]. Затем по значениям X₁[k] и X₂[k] определяют требуемое N–точечное ДПФ X[k]. Если последняя операция будет выполняться просто и не потребует сложных вычислений, то для вычисления N – точечного ДПФ потребуется выполнить (N/2)²+(N/2)²=N²/2 операций. Если продолжить процесс разбиения x₁[n] и х₂[n] на две и находить для каждой из них свои ДПФ, то можно существенно сократить количество операций.

Рассмотрим ДПФ последовательности x[n]:

где  – вспомогательная функция.

Разобьем x[n] на две части x₁[n] и х₂[n], содержащие соответственно четные и нечетные члены x[n]:

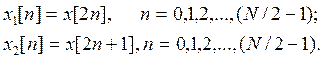
Тогда

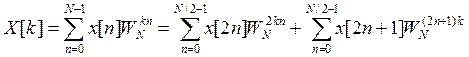
Так как , то

.

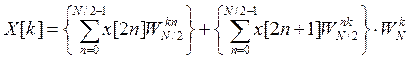Здесь выражения в фигурных скобках представляют прямые N/2 – точечные ДПФ от последовательностей x₁[n] и х₂[n]. Тогда,

Из формулы (5a.2) следует, что N – точечное ДПФ X[k] может быть вычислено через два N/2 – точечных ДПФ X₁[k] и X₂[k]. Следует иметь в виду, что отсчеты ДПФ для последовательностей х₁[n] и х₂[n] повторяются с периодом N/2. Поэтому

Учитывая равенство , из (5a.2) получаем выражение для определения второй части последовательности спектральных коэффициентов X[k]:

Формулы (5a.2), (5a.4) представляют базовую операцию БПФ (так называемую «бабочку»). Схематическое изображение "бабочки" показано на рис. 5a.1. Здесь кружок в центре обозначает операцию сложения/вычитания. Стрелка обозначает операцию умножения на . Жирные точки обозначают ячейки памяти, содержащие входные и выходные значения для отдельных этапов БПФ.

На рис. 5a.2 показана схема вычисления 8 – точечного БПФ с использованием двух 4 – точечных преобразований.

В свою очередь, 4 – точечные преобразования могут быть определены через 2 – точечные, которые вычисляются по формулам:

На рис. 5a.3 показан результирующий граф 8 – точечного БПФ.

Описанный алгоритм БПФ называется алгоритмом с прореживанием по времени, так как здесь требуется перестановка входных значений x[n] (см. рис. 5a.3). Алгоритмы, при реализации которых требуется перестановка отсчётов X[k], называются алгоритмами с прореживанием по частоте.

Поскольку произведение  можно после вычисления запомнить, то для каждой базовой операции БПФ необходимо выполнять только умножение X₂[k] на множитель W_N^k. Входные и выходные значения базовых операций обычно хранят в одних и тех же ячейках памяти. На одну базовую операцию приходится одна дополнительная ячейка для хранения произведения . Поэтому входная x[n] и выходная X[k] последовательности, а также промежуточные результаты могут размещаться в одном и том же массиве ячеек памяти. Алгоритм БПФ, использующий указанные возможности, называют алгоритмом с замещением.

Особенностью рассматриваемых алгоритмов БПФ является необходимость перестановки входных или выходных значений. Элементы входной последовательности для алгоритма с прореживанием по времени должны быть расположены в памяти в бит–инверсном порядке. Бит–инверсный порядок задается путем «зеркального» отображения двоичных разрядов входной последовательности (табл. 5a.1).

Таблица 5а.1 – Бит–инверсный порядок