ФСППС
Первый вариант выбирают студенты, у которых номер зачетной книжки (студенческого билета) заканчивается четной цифрой
Второй вариант выбирают студенты, у которых номер зачетной книжки (студенческого билета) заканчивается нечетной цифрой
КОНТРОЛЬНАЯ №1 РАБОТА ПО ЛИНЕЙНОЙ АЛГЕБРЕ
Вариант 1
1. Решить уравнение А2 – 2(ВТ × С)Т = DT×X, где
А= ,
,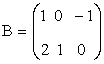 ,
,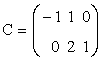 ,D=
,D=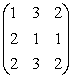
2. Решить систему уравнений методом Крамера
3х1 + 4х2 – 2х3 = 16
-5х1 + х2 + 6х3 = -1
7х1 - 5х2 + х3 = 0
1. Решить уравнение А2 – (В ×СТ)Т = ХDT, где
А=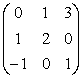 ,
,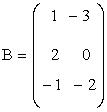 ,
,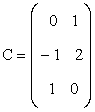 ,D=
,D=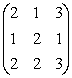
2. Решить систему уравнений методом Крамера
7х1 + 2х2 – 3х3 = 17
-4х1 + 2х2 + 4х3 = -2
9х1 - х2 - 6х3 = 14
КОНТРОЛЬНАЯ №2 РАБОТА ПО ЛИНЕЙНОЙ АЛГЕБРЕ
Вариант № 1
1. Найти решение системы уравнений методом Гаусса
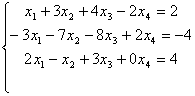
2. Найти собственные числа и собственные столбцы матрицы
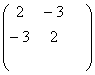
3. Найти площадь треугольника, проходящего через точки А(2,4,-1), В(3,1,5)
и точку С(5,1,-7)
4. Даны вершины тетраэдра с координатами А(5,2,2),В(-8,-2,5),C(6,3,0),D(9,3,2).
Найти длины высоты, опущенной из вершины D на основание тетраэдра.
Вариант № 2
1. Найти решение системы уравнений методом Гаусса
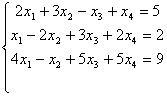
2. Найти собственные числа и собственные столбцы матрицы
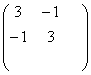
3. Найти площадь треугольника, проходящего через точки А(2,4,-1), В(3,1,5)
и точку С(5,1,-7)
4. Даны вершины тетраэдра с координатами А(4,5,-3), В(6,3,0), C(8,5,-9),
D(-3,-2,-10). Найти длины высоты, опущенной из вершины D на основание
тетраэдра.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.