Комбинационные схемы и конечные автоматы. Синтез конечных автоматов (Глава 2 учебного пособия "Основы электронной вычислительной техники и программирования")

Г Л А В А    2

КОНЕЧНЫЕ АВТОМАТЫ

2.1  Комбинационные схемы и конечные автоматы

В ЦВМ преобразование дискретной информации производится электронными устройствами (логическими схемами) двух типов: комбинационными схемами и конечными автоматами.

Комбинационной схемой называют устройство, совокупность выходных символов которого (выходное слово) в каждый дискретный момент времени  однозначно определяется совокупностью входных символов (входным словом), поступившей на вход устройства в тот же момент времени .

Рассмотрим комбинационную схему (рис.2.1), имеющую n входов и m выходов.

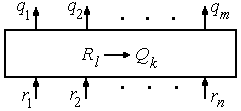
Рис.2.1. Комбинационная схема

Пусть на каждый из n входов этого устройства может быть подан один символ из конечного алфавита

                                              (2.1)

а на каждом из m выходов может быть получен один символ  из конечного алфавита

                                           (2.2)

Это означает, что каждое входное слово  образуется из n символов входного алфавита X, а каждое выходное слово  – из m символов выходного алфавита .

Таким образом, для устройства типа комбинационной схемы результат обработки входной информации (выходное слово ) зависит только от комбинации сигналов на входах (входного слова ).

Соответствие выходного слова входному может быть задано аналитически в виде:

                                           (2.3)

   . . . . . . . . . . . . . .

В ЦВМ алфавиты X и Y состоят всего из двух символов: 0 и 1. В этом случае функции  являются переключательными функциями и к их анализу и синтезу может быть применен аппарат булевой алгебры.

Конечным автоматом (рис.2.2) называют устройство, выходное слово которого в дискретный момент времени  определяется не только по входному слову, поступившему в тот же момент времени , но и по внутреннему состоянию устройства, обусловленному его предшествующей работой. Для некоторых устройств внутренним состоянием может быть предыдущее выходное слово.

Для конечного автомата кроме входного и выходного алфавитов задаются еще одним конечным алфавитом

,                                             (2.4)

который называют алфавитом внутренних состояний, а символы  – внутренними состояниями.

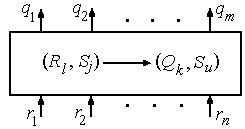
Рис.2.2. Конечный автомат

В реальных условиях входные и выходные сигналы представляют собой непрерывные функции времени, поэтому для надежного различения сигналов требуется, чтобы новые значения на входах устройства появлялись после окончания переходных процессов, связанных с предыдущими значениями. При рассмотрении логической структуры автоматов обычно отвлекаются от существа этих процессов и считают, что переменные изменяются не непрерывно, а мгновенно в некоторые моменты времени, называемые тактами. Интервалы  между тактами могут быть различными, но мы будем полагать их постоянными и равными . Предполагается, что тактовые моменты  определяются синхронизирующими сигналами. Таким образом, вводится понятие дискретного автоматного времени , где  причем переменные зависят не от физического времени, а от номера такта , т.е. вместо непрерывных функций  рассматриваются дискретные значения .

Для задания конечного автомата необходимо установить соответствие между всеми парами  в момент времени  и парами  в момент времени .

2.2  Типы конечных автоматов

В технике с понятием автомата обычно связывается некоторое устройство, способное выполнять определенные функции без вмешательства человека или с его ограниченным участием. Такое понимание автомата является слишком узким. В широком смысле конечный автомат – это математическая модель, отображающая физические или абстрактные явления самой разнообразной природы. Такая модель успешно используется как в технике, так и в других областях (лингвистике, теории