MatLab Script. Функции для вызова диалоговых окон

MatLab Script

Скриптовый файл в MatLab – это набор операций и последовательных вызовов функций, в которые передаются самим скриптом входные данные. Т.е., если написать несколько функций, которые будут реализовать тот или иной метод, а потом в рабочей области MatLab присваивать именам переменным значения с последующим вызовом этих функций, то те же результаты можно получить, создав скриптовый файл, записав в него все то, что было записано ранее в рабочей области, и вызвав этот скрипт. Тем самым вы вместо того, чтобы постоянно присваивать (переприсваивать) значения, просто вызываете одну функцию. Это существенно облегчает тестирование и скорость работы с вашим продуктом.

В MatLab существует множество функций , с помощью которых можно намного упростить работы с вашей программой и придать ей более удобный и дружелюбный интерфейс. Для того, чтобы превратить программу, написанную вами из «консольного» вида в «оконный» необходимо воспользоваться диалоговыми окнами. Наиболее используемые из них – это:

1. inputdlg – функция, для вызова диалогового окна для ввода данных.

Синтаксис написания:

prompt = {'А:','В:','C:'};

dlg_title = 'Input';

num_lines = 1;

def = {'1','2','3'};

, где

prompt – это вектор, в котором хранится содержания строк, которые будут находиться слева от полей для ввода

dlg_title – это переменная, в которой хранится название вашего диалогового окна(русские названия не поддерживает).

num_lines – это переменная отвечает за то, сколько возможно будет написать строк в одном поле для ввода.

def – это вектор, в котором находятся значения по умолчанию для каждого поля для ввода.

Для того чтобы получить значения, записанные пользователем необходимо присвоить сначала переменной то, что возвращает inputdlg, и обращаться к ней, как к вектору:

answer = inputdlg(prompt,dlg_title,num_lines,def);

a = answer{1};

b = answer{2};

c = answer{3};

2. questdlg - функция, для вызова диалогового окна, которое содержит несколько кнопок, и передает название выбранной пользователем кнопки.

Синтаксис написания:

question = 'Выберите вариант:';

name = 'Варианты';

var_a = 'А';

var_b = 'B';

var_c = 'C';

choise = questdlg(question, name, var_a, var_b, var_c, var_a);

Последняя переменная, которая передается в функцию означает какая из кнопок будет предложена(подсвечена) по умолчанию.

После того, как пользователь выберет, например, вариант В, в переменную choise будет записано 'B'.

Потом эту переменную можно использовать для организации условного оператора или switch-case оператора.

Замечание. Если название кнопок будет разное по длине, то при проверке choise=='text' и значение в choise не будет длиною в 4 символа появиться ошибка. Для того чтобы избежать этого можно воспользоваться функциями сравнения строковых данных или, если у вас, например, первый символ всех кнопок уникальный, сравнивать только по этому символу, например:

choise = questdlg(results,'Интегрирование', 'Показать график функции', 'Выход', 'Показать график функции');

if(choise(1)=='П') 

    fplot(func,[a,b]);

end;

Теперь рассмотрим более сложный пример – реализацию скриптового файла для Интегрирования методом Чебышева и Гаусса:

function res = CheGau()

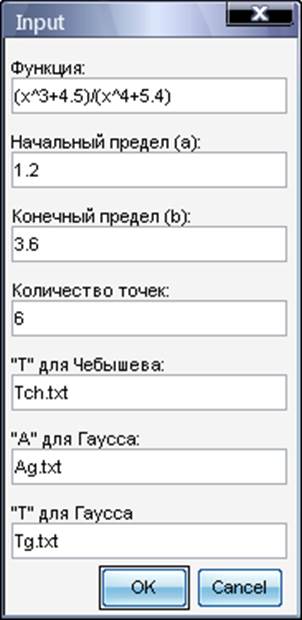
prompt = {'Функция:','Начальный предел (а):','Конечный предел (b):', 'Количество точек:', '"T" для Чебышева:', '"A" для Гаусса:', '"T" для Гаусса'};

dlg_title = 'Input';

num_lines = 1;

def = {'(x^3+4.5)/(x^4+5.4)','1.2','3.6', '6', 'Tch.txt', 'Ag.txt', 'Tg.txt'};

answer = inputdlg(prompt,dlg_title,num_lines,def);

func = answer{1};

a = str2num(answer{2});

b = str2num(answer{3});

n = str2num(answer{4});

Tch = CheGau_ReadFile(answer{5});

Ag = CheGau_ReadFile(answer{6});

Tg = CheGau_ReadFile(answer{7});

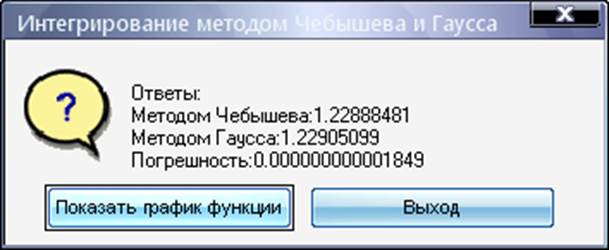
results{1} = 'Ответы:';

results{2} = strcat('Методом Чебышева: ',...

num2str(CheGau_Chebish(func, a, b, n, Tch),'%.8f'));

results{3} = strcat('Методом Гаусса: ', ...

num2str(CheGau_Gauss(func, a, b, n, Ag, Tg),'%.8f'));

results{4} = strcat('Погрешность: ',...

 num2str(CheGau_Rn(func, a, b, n),'%.15f'));

choise = questdlg(results,'Интегрирование методом Чебышева и Гаусса', 'Показать график функции', 'Выход', 'Показать график функции');

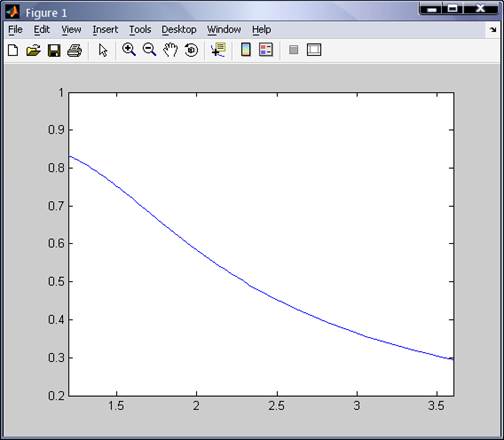
if(choise(1)=='П') 

    fplot(func,[a,b]);

end;

В результате получиться: