кафедра 304
Лабораторная работа № 7
по предмету «Численные методы»
по теме: Интерполирование для таблиц с постоянным с шагом. Численное дифференцирование. Обратное интерполирование.
Выполнила студентка 325 гр.
Старцева А. В.
Проверила ст. преподаватель каф. 304
Яровая О. В.
______________________
Теоретические сведенья
Ручной счет
Расчет в пакете Mathcad
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Численное дифференцирование
|
|
|
|
|
|
|
|
|
|
|
|
Обратное интерполирование
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Расчет в пакете Matlab
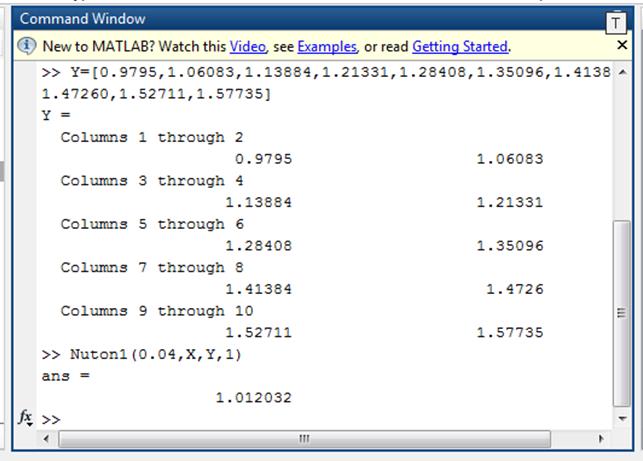
Первая интерполяционная формула Ньютона:
function res = Nuton1(x,X,Y,n);
res=Y(1);
h=X(2)-X(1);
for i=1:n
konrazn=diff(Y,i);
konrazn=konrazn(1);
fact=prod(1:i);
Mult=1;
for j=1:i
Mult=Mult*(x-X(j));
end;
res=res+(konrazn/fact*h^i)*Mult;
end;
return
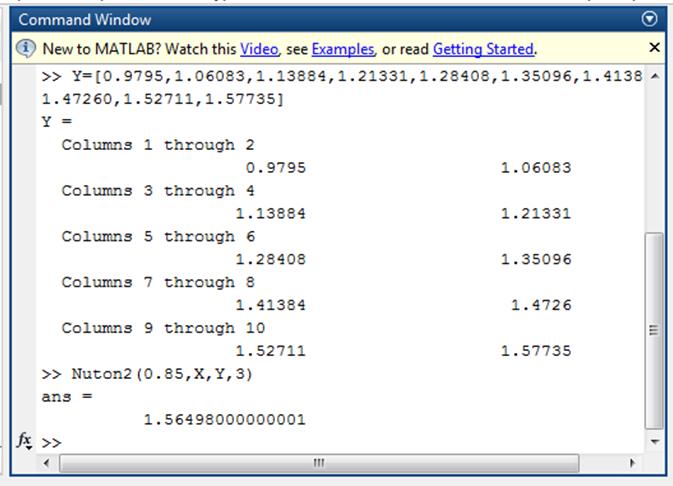
Вторая
интерполяционная формула Ньютона:
function res =
Nuton2(x,X,Y,n);
res=Y(n);
h=X(2)-X(1);
q=(x-X(n))/h;
for i=1:(n-1)
konrazn=diff(Y,i);
konrazn=konrazn(n-i);
fact=prod(1:i);
Mult=1;
for j=0:(i-1)
Mult=Mult*(q+j);
end;
res=res+(konrazn/fact)*Mult;
end;
return
Функция вычисляет значения указанного полинома в заданном множестве точек
function yy = EvalNuton(X,Y,xx,formNumber)
n=length(X)-1;
if (formNumber==1)
for i=1:length(xx);
yy(i)=Nuton1(xx(i),X,Y,n);
end;
else
for i=1:length(xx);
yy(i)=Nuton2(xx(i),X,Y,n+1);
end;
 end;
end;
return
Построение графика:
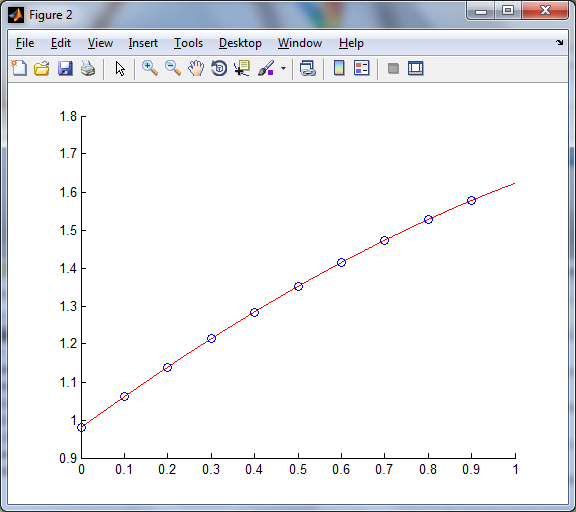
Скрипт файл:
function rts = Ch(x,X,Y,n)
choise = questdlg('Выберите формулу интерполяции:', 'Формула Ньютона', '1','2','1');
switch choise
case '1'
rts=Nuton1(x,X,Y,n);
case '2'
rts=Nuton2(x,X,Y,n);
end
end
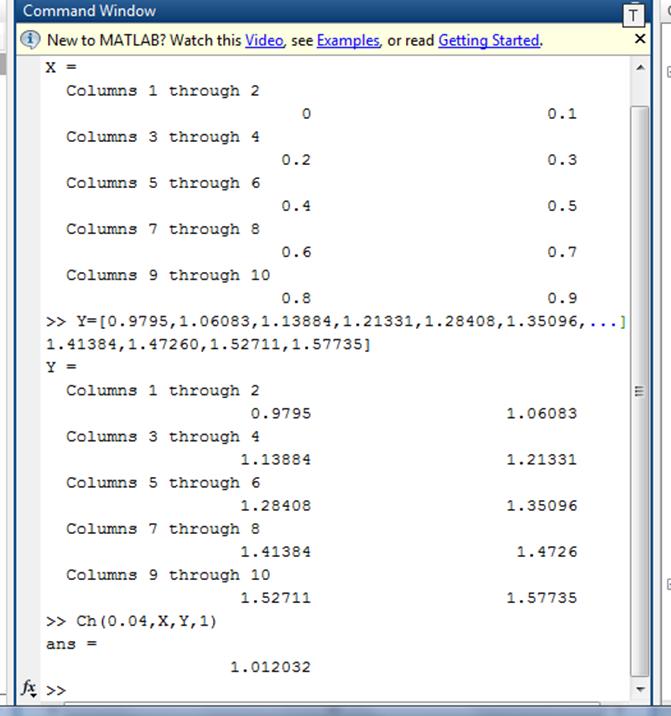
Обратное интерполирование
function res=iter(y,Y,X,eps)
h = X(2)-X(1);
n = length(X);
konrazn=diff(Y,1);
konrazn=konrazn(1);
q = (y - Y(1))/konrazn;
q_next = Q(q,y,Y,n);
while abs(q_next-q)>eps
q=q_next;
q_next = Q(q,y,Y,n);
end;
res = q_next*h+X(1);
return
% функция Q(q,y,Y,n):
function res=Q(q,y,Y,n)
sum = 0;
for i=2:n-1
% вычисление конечной разности
konrazn=diff(Y,i);
konrazn=konrazn(1);
% вычисление факториала
fact=prod(1:i);
% вычисляем (x-y0)(x-y)...(x-y)
Mult=1;
for j=1:i
Mult=Mult*(q-j+1);
end;
sum=sum+(konrazn/(fact))*Mult;
end;
konrazn=diff(Y,1);
konrazn=konrazn(1);
res = (y-Y(1)-sum)/konrazn;
return
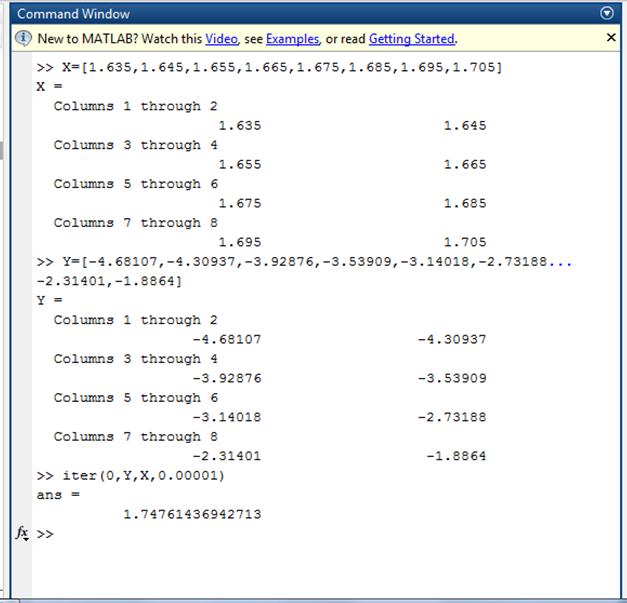
Вывод:
на этой лабораторной работе я изучила формулы интерполяции для таблиц с
постоянным шагом; научилась решать задачи численного дифференцирования и
обратного интерполирования. Вычислила приближено для заданной функции значения
в неузловых точках с помощью ручного счета (![]() ), с помощью пакетов Mathcad (
), с помощью пакетов Mathcad (![]() ) и Mathlab (
) и Mathlab (![]() ).А так же значение производной в точке
х=0.85, (f ′(х)= 2.32762). Нашла корень
уравнения у =
).А так же значение производной в точке
х=0.85, (f ′(х)= 2.32762). Нашла корень
уравнения у = ![]() методом обратной интерполяции (х=1.74658) и
проверила с помощью встроенной функции.
методом обратной интерполяции (х=1.74658) и
проверила с помощью встроенной функции.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.