Экзаменационные вопросы и практические задания дисциплины "Теория вероятностей и математическая статистика" (Различные виды сходимости последовательностей случайных величин. Построить доверительный интервал с надежностью 0.95 для дисперсии нормальной генеральной совокупности)

1.  Различные виды сходимости последовательностей случайных величин. Связь между ними.

2.  Статистическая проверка гипотез. Общие определения.

3.  Смещенная и несмещенная оценки дисперсии.

4.  Многомерное нормальное распределение.

5.  Свойство многом норм

6.  Сумма норм велич

7.  Сумма пуассое

8.  Свертка распр коши

9.  Односторонние и двусторонние критические области.

10.Неравенство Маркова. Неравенство Чебышева.

11.Закон больших чисел.

12.Теоремы Чебышева и Маркова.

13.Характеристическая функция и её свойства.

14.Основные понятия математической статистики.

15.Доверительный интервал для дисперсии нормальной генеральной совокупности.

16.Доверительный интервал для среднего нормальной генеральной совокупности при известной дисперсии.

17.Доверительный интервал для среднего нормальной генеральной совокупности при неизвестной дисперсии.

18.Закон распределения выборочной дисперсии(хи квадрат с н-1 степ. Свободы)

19.Ди для показательного и биномиального зр.

20.Элементы проверки статист гипотез(ошибки 1, 2 рода)

21.Теорема Пирсоа(без док-ва)

22.Выборочн. Коэф корреляции

23.МНК( в практике)

24.Критерий Колмагорова.

25.Центральная предельная теорема для сумм независимых одинаково распределенных случайных величин.

26.Терема Ляпунова и неравенство берри-эссеина

27.Распределения  и .

28.Эмпирическая функция распределения. Гистограмма.

29.Проверка гипотезы о виде распределения генеральной совокупности. Критерий .

30.Постановка задачи и основное уравнение однофакторного дисперсионного анализа((а+б)в квадрате=)

31.Распределение сумм независимых случайных величин. Использование характеристической функции.

32.Элементы теории портфеля(в случае двух акций, матричный вид)

33.Точечные оценки неизвестных параметров распределений. Свойства оценок.

34.Достаточное условие состоятельности

35.Метод максимального правдоподобия. Пример: ОМП параметров нормального распределения.(Норм, пуасс, показательный, паретто, Реллея, биномиальный)

36.Проверка гипотезы о виде распределения генеральной совокупности. Критерий Колмогорова.

37.Статистическая оценка коэффициента корреляции.

38.Элементы теории Марковитца. ВНИМАНИЕ! Для трех групп разные акценты.

39.Нахождение параметров линейной регрессии. ВНИМАНИЕ! Для трех групп разные акценты.

40.Проверить выполнение закона больших чисел для последовательности независимых величин

41. Найти характеристическую функцию распределения Пуассона.

42. Найти условный закон распределения и вычислить условное математическое ожидание второй СВ при условии, что первая приняла значение 2.

43. Построить доверительный интервал для дисперсии нормальной генеральной совокупности при доверительной вероятности 0.90, если объем выборки равен 9, несмещенная оценка дисперсии равна 20.

44. Построить доверительный интервал при доверительной вероятности  0.95 для среднего нормальной генеральной совокупности при неизвестной дисперсии, если объем выборки равен 25, выборочное среднее равно 16, несмещенная оценка дисперсии равна 16. 

45. Построить доверительный интервал для дисперсии нормальной генеральной совокупности при доверительной вероятности 0.95, если объем выборки равен 16, несмещенная оценка дисперсии равна 0.81  

46. Проверить, что последовательность независимых величин сходится к нулю в среднем  порядка

47. Найти характеристическую функцию случайной величины, имеющей равномерное распределение.

48. Построить доверительный интервал при доверительной вероятности  0.95 для среднего нормальной генеральной совокупности при неизвестной дисперсии, если объем выборки равен 10, выборочное среднее равно 9.3, несмещенная оценка дисперсии равна 0.1.

49.Найти характеристическую функцию суммы  независимых одинаково распределенных случайных величин,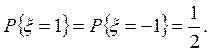

50.Проверить, что последовательность сходится к нулю в среднеквадратичном

37. Проверить, что последовательность независимых величин подчиняется закону больших чисел, если их распределение задано таблицей

38. Найти характеристическую функцию показательного распределения.

39. Найти если слагаемые имеют равномерное распределение на отрезке от 0 до 2.

40. Поставщик арбузов утверждает, что процент зеленых равен 10. Реализатор считает, что зеленых 20%. Проверяют 10 арбузов. Если число зеленых не более 2, партию принимают на условиях поставщика. Найти вероятности ошибок 1 и 2 рода.

41. Проверить, что выполняется закон больших чисел

42. Проверяется гипотеза о среднем нормальной генеральной совокупности. При уровне значимости 0.05 проверить гипотезу  а=24 при альтернативе a>24, если объем выборки равен 25, выборочное среднее равно 27, несмещенная оценка дисперсии 36.

43.  Построить график эмпирической функции распределения по выборке 3,3-2,-1,-2,-1,0,0,0,0,3. Найти точечные оценки среднего и дисперсии.

44. Найти условный закон распределения и вычислить условное математическое ожидание второй случайной величины при условии, что первая приняла значение 2.

45. Проверить, что последовательность независимых величин подчиняется закону больших чисел, если их распределение задано таблицей