1. Гауссовский процесс.
2. Эргодическая теорема для цепей Маркова.
3. Найти
корреляционную функцию случайного процесса ![]() , где
, где ![]() имеет равномерное распределение на отрезке
имеет равномерное распределение на отрезке
![]() и не зависит от процесса
и не зависит от процесса ![]() , имеющего корреляционную функцию
, имеющего корреляционную функцию ![]() .
.
4. Нормальний стаціонарний випадковий процес має нульове математичне
сподівання й кореляційну функцію 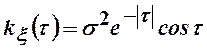 . Записати вирази його одновимірних і двовимірних щільностей. Знайти
ймовірності випадкових подій
. Записати вирази його одновимірних і двовимірних щільностей. Знайти
ймовірності випадкових подій ![]() і
і 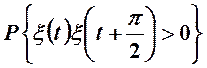 .
.
![]()
![]() ,
, ![]()
![]() . Найти
. Найти![]() , если
, если ![]()
1. Марковский однородный процесс со счетным числом состояний.
2. Случайная гармоника.
3. Розглянемо випадковий процес ![]() , де
, де ![]() -процес
Пуассона із параметром l.
Довести, що
-процес
Пуассона із параметром l.
Довести, що ![]() ,
,![]() . Довести, що
. Довести, що ![]() .
.
4.
Дискретні
випадкові величини ![]() і
і ![]() є
незалежними й мають однаковий розподіл
є
незалежними й мають однаковий розподіл ![]() .
Знайти одновимірні розподіли випадкового процесу
.
Знайти одновимірні розподіли випадкового процесу ![]() у два
моменти часу
у два
моменти часу ![]() і
і 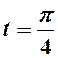 . Записати
кореляційну функцію. Переконатись в тому, що процес є стаціонарним у широкому
змісті і не є стаціонарним у вузькому змісті.
. Записати
кореляційну функцію. Переконатись в тому, що процес є стаціонарним у широкому
змісті і не є стаціонарним у вузькому змісті.
1. Классификация Кендалла
2. Определение марковского момента. Тождества Вальда.
3. Довести стаціонарність процесу ![]() , де
, де ![]() та
та ![]() - незалежні випадкові
величини,
- незалежні випадкові
величини, ![]() має рівномірний розподіл на
має рівномірний розподіл на ![]() ,
, 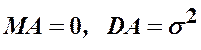 .
.
4.
Знайти розподіл випадкової величини ![]() , де
, де ![]() .
.
1. .
2. Основные понятия теории случайных процессов.
3.
Нехай ![]() , де доданки є
незалежними величинами, що набувають значень +1 та -1 із ймовірністю ½.
Довести, що
, де доданки є
незалежними величинами, що набувають значень +1 та -1 із ймовірністю ½.
Довести, що ![]() - мартингал
- мартингал
4.
Центрований
стаціонарний процес має кореляційну функцію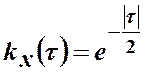 .
Знайти
.
Знайти ![]() і
і ![]() .
.
1. Стационарность процессов в широком и узком смысле.
2. Процессы с независимыми приращениями.
3.
Корреляционная функция гауссовского процесса равна ![]() . Среднее значение равно 2. Найти
. Среднее значение равно 2. Найти 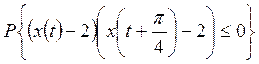 .
.
4.
Довести, що 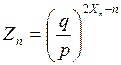 - мартингал, якщо
- мартингал, якщо ![]() ,
, ![]()
1. Цепи Маркова. Основные понятия и примеры.
2.
3. .
4.
Найти стационарные вероятности для системы ![]() .
.
5.
Довести, що 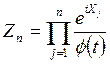 - мартингал, якщо
- мартингал, якщо ![]() для незалежних величин із однаковим
розподілом.
для незалежних величин із однаковим
розподілом.
1. Пуассоновский поток.
2. Мартингалы с непрерывным временем.
3.
Начальное распределение цепи Маркова задано вектором (0.9,0.1). Матрица
переходных вероятностей 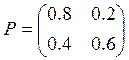 . Найти стационарное
распределение и распределение вероятностей по состояниям в момент времени 2.
. Найти стационарное
распределение и распределение вероятностей по состояниям в момент времени 2.
4.
Найти основные характеристики процесса, ![]() если
случайные величины
если
случайные величины ![]() и
и ![]() имеют
одинаковые средние значения 1 и матрицу ковариаций
имеют
одинаковые средние значения 1 и матрицу ковариаций 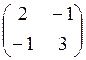 .
.
1.
Распределение времени начала обслуживания в системе ![]() .
.
2.
Процес ![]() називається процесом
Орнштейна-Уленбека із параметрами
називається процесом
Орнштейна-Уленбека із параметрами ![]() . Довести, що він
стаціонарний.
. Довести, що він
стаціонарний.
4.
5. Определение стационарных процессов.
1. Связь понятий стационарности в широком и узком смыслах.
2.
Найти характеристики процесса ![]() , где средние значения
случайных величин равны 2 и 3, а матрица ковариаций имеет вид:
, где средние значения
случайных величин равны 2 и 3, а матрица ковариаций имеет вид: 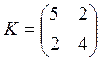 .
.
3. Работают три независимых элемента, каждый из которых может отказать с вероятностью 1/2. По окончании суток один неисправный элемент меняют на исправный. Случайный процесс-число неисправных элементов в момент начала цикла. Записать матрицу переходных вероятностей. Найти стационарное распределение.
1.
Система ![]() .
.
2. Обобщенный пуассоновский процесс.
3. Согласно классификации по предпочтительному виду трудовой деятельности, люди делятся на так называемых «сциентиков», «райтеров», «трейдеров», и «продакторов». Предположим, в городе среди 30-летних жителей соотношение этих типов равно 0.1:0.2:0.4:0.3. Пусть сын сохраняет тип, присущий отцу, с вероятностями соответственно 0.7, 0.4, 0.7 и 0.4, и меняет тип на любой другой с одинаковыми вероятностями. Найти процентное соотношение типов в следующем поколении и стационарное распределение.
4.
Нехай ![]() - процес Пуассона.
Знайти
- процес Пуассона.
Знайти ![]()
![]() .
.
Экзаменационный билет №18(упрощенный)
1. Определение и примеры цепей Маркова.
2. Стационарные процессы.
3.
Матриця переходу однорідного ланцюга Маркова за один крок
складає 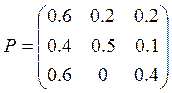 . Знайти стаціонарний розподіл, знайти
матрицю ймовірностей переходу за два кроки. Знайти ймовірність переходу із
стану 2 у стан 3 за два кроки.
. Знайти стаціонарний розподіл, знайти
матрицю ймовірностей переходу за два кроки. Знайти ймовірність переходу із
стану 2 у стан 3 за два кроки.
4.
Определить, является ли случайный процесс![]() стационарным,
если случайные величины
стационарным,
если случайные величины ![]() и
и ![]() некоррелированы, имеют математические
ожидания, равные нулю и дисперсии 4 и 9.
некоррелированы, имеют математические
ожидания, равные нулю и дисперсии 4 и 9.
Экзаменационный билет №19(упрощенный)
1. Основные характеристики случайных процессов.
2. Пуассоновский поток.
3.
Найти стационарное распределение и вероятность перехода из состояния 0 в
состояние 1 за два шага для цепи Маркова, заданной матрицей переходных
вероятностей 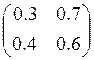 .
.
4.
Найти среднее и корреляционную функцию процесса ![]()
![]() ,
, 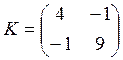 .
.
Утвержден на заседании кафедры 405. Протокол № от .12.10 -
Экзаменационный билет №20(упрощенный)
1. Основные типы случайных процессов.
2. Цепь Маркова.
3.
Найти стационарное распределение и вероятность перехода из состояния 1 в
состояние 1 за два шага для цепи Маркова, заданной матрицей переходных
вероятностей 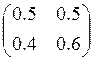 .
.
4.
Довести, що ![]() , якщо
, якщо ![]() - випадковий процес,
- випадковий процес, ![]() та
та ![]() -
невипадкові функції,
-
невипадкові функції, ![]() .
.
Экзаменационный билет №21(упрощенный)
1. Винеровский процесс.
2. Определение и простейшие примеры мартингалов.
3.
Найти характеристики процесса ![]() , где средние значения
случайных величин равны 0 и -2, а матрица ковариаций имеет вид:
, где средние значения
случайных величин равны 0 и -2, а матрица ковариаций имеет вид: 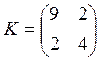 .
.
4. Составить матрицу переходных вероятностей цепи Маркова за один шаг для одномерного симметричного случайного блуждания по точкам 0,1,2,3,4 с полупоглощающими экранами в точках 0 и 4: вероятность остаться в точках равна 0.4, вероятность выйти из них равна 0.6. Найти вероятность перехода из точки 2 в точку 4 за два шага.
Экзаменационный билет №24
1. Винеровский процесс.
2. Задача о разорении: вероятность разорения игрока для случая справедливой игры. Средняя продолжительность игры.
3. Найти
вероятность того, что за время ![]() поступит четное число
точек пуассоновского потока.
поступит четное число
точек пуассоновского потока.
4.
Матриця переходу однорідного ланцюга Маркова за один крок
складає 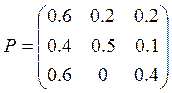 . Знайти стаціонарний розподіл, знайти
матрицю ймовірностей переходу за два кроки. Знайти ймовірність переходу із
стану 2 у стан 3 за два кроки.
. Знайти стаціонарний розподіл, знайти
матрицю ймовірностей переходу за два кроки. Знайти ймовірність переходу із
стану 2 у стан 3 за два кроки.
1. Стационарность в широком и узком смысле.
2. Система уравнений Колмогорова-Чэпмена для вероятностей пребывания Марковского процесса в состояниях.
3. Найти
распределение вероятностей по состояниям в момент времени 2, если начальное
распределение задано вектором (0.2,0.8), а матрица вероятностей перехода цепи
Маркова за 1 шаг 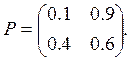
4. Нехай ![]() - два незалежні один від одного
стаціонарні процеси. Відомо, що
- два незалежні один від одного
стаціонарні процеси. Відомо, що ![]() ,
, ![]() . Знайти кореляційну функцію процесу
. Знайти кореляційну функцію процесу ![]() .
.
1. Процесс Орнштейна-Уленбека.
2.
Скласти систему рівнянь Колмогорова-Чепмена для
стаціонарних ймовірностей системи ![]() , якщо клієнт, що
зустрів у системі
, якщо клієнт, що
зустрів у системі ![]() клієнтів, залишається із
ймовірністю
клієнтів, залишається із
ймовірністю ![]() .
.
3.
Найти одномерные плотности случайного процесса ![]() , если
, если ![]() .
.
Экзаменационный билет №32
1. Процессы с независимыми приращениями.
2. Стационарность случайных процессов.
3.
Составить систему уравнений Колмогорова-Чэпмена в задаче о снабжении
энергией: имеется ![]() независимых потребителей, каждый
за время
независимых потребителей, каждый
за время ![]() подключается к системе с вероятностью
подключается к системе с вероятностью ![]() и выключается с вероятностью
и выключается с вероятностью ![]() . Решить систему для стационарных
вероятностей.
. Решить систему для стационарных
вероятностей.
4.
Найти распределение вероятностей по состояниям в момент времени 1, если
начальное распределение задано вектором (0.4,0.6), а матрица вероятностей
перехода цепи Маркова за 1 шаг 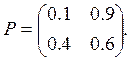
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.