














 39. 1 способ.
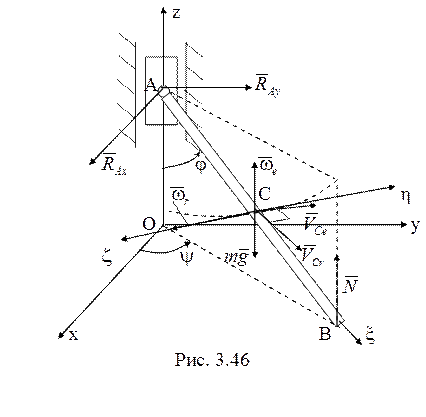
Рассматриваемая система (рис. 3.46) имеет две степени свободы. В качестве обобщенных
координат, описывающих положение системы, возьмем углы
39. 1 способ.
Рассматриваемая система (рис. 3.46) имеет две степени свободы. В качестве обобщенных
координат, описывающих положение системы, возьмем углы ![]() и
и
![]() . Уравнения движения системы будем составлять
так, чтобы они не содержали неизвестных сил реакции связей
. Уравнения движения системы будем составлять
так, чтобы они не содержали неизвестных сил реакции связей ![]() .
.
Главный момент внешних
сил ![]() , поэтому составляющая кинетического
момента
, поэтому составляющая кинетического
момента ![]() . Кинетический момент
. Кинетический момент ![]() . Взяв в качестве переносного движения
стержня поворот вокруг оси
. Взяв в качестве переносного движения
стержня поворот вокруг оси ![]() плоскости
плоскости ![]() , а в качестве относительного – движение
стержня в этой плоскости, найдем, что
, а в качестве относительного – движение
стержня в этой плоскости, найдем, что
![]() .
.
Кинетический момент стержня относительно центра масс
![]() . (3.57)
. (3.57)
Расположение связанных осей ![]() показано на рис. 3.46. Моменты инерции
показано на рис. 3.46. Моменты инерции 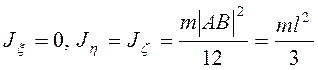 . Угловая скорость также находится по
теореме сложения
. Угловая скорость также находится по
теореме сложения
![]() . (3.58)
. (3.58)
Учитывая (3.57) и (3.58), получим  , и
, и
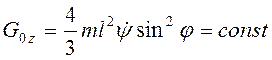 .
.
В начальный момент времени  , т.е.
, т.е. 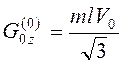 , и
, и
 . (3.59)
. (3.59)
Так как работу совершает только консервативная стационарная сила тяжести, то выполнен закон сохранения механической энергии
![]() . (3.60)
. (3.60)
Кинетическая энергия 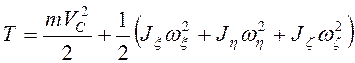 . Для скорости центра масс
. Для скорости центра масс ![]() , и
, и  . Потенциальная
энергия
. Потенциальная
энергия ![]() . Подстановка последних выражений в (3.60)
с учетом начальных условий даст
. Подстановка последних выражений в (3.60)
с учетом начальных условий даст
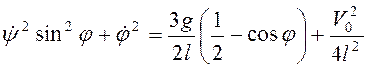 . (3.61)
. (3.61)
Условие отрыва стержня от
плоскости ![]() соответствует обращению в ноль реакции
пластины
соответствует обращению в ноль реакции
пластины ![]() . По теореме о движении центра масс
. По теореме о движении центра масс ![]() . Так как
. Так как ![]()
![]() , то
, то
![]() . (3.62)
. (3.62)
Согласно (3.59):  , учитывая это из (3.61) получим
, учитывая это из (3.61) получим
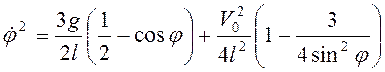 .
.
Дифференцированием последнего выражения по времени получим
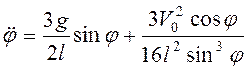 .
.
Подставляя найденные выражения в (3.62) получаем для реакции опоры
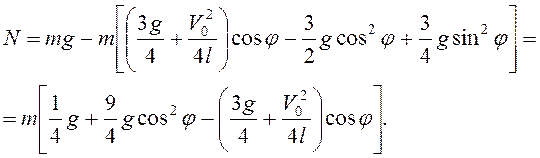
При ![]()
![]() , и отрыв наступает в начальный момент
времени. При
, и отрыв наступает в начальный момент
времени. При ![]() реакция опоры обращается в ноль
при значении угла
реакция опоры обращается в ноль
при значении угла ![]() :
: 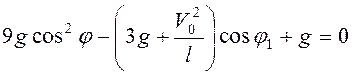 , т.е.
, т.е.
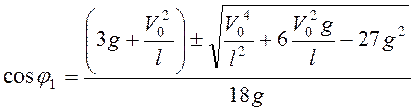 .
.
Отрыв произойдет при ![]() :
: ![]() .
.
2-й способ. Уравнение Лагранжа второго рода по
обобщенной координате ![]() имеет вид
имеет вид  . Следовательно
. Следовательно 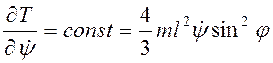 , что
сразу дает (3.59). Далее ход решения из первого способа повторяется.
, что
сразу дает (3.59). Далее ход решения из первого способа повторяется.
Ответ: если ![]() , то
, то ![]() ; если
; если ![]() , то
, то
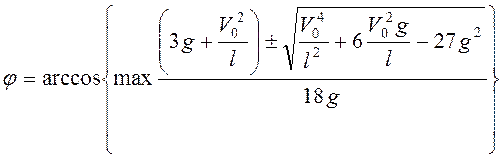 .
.
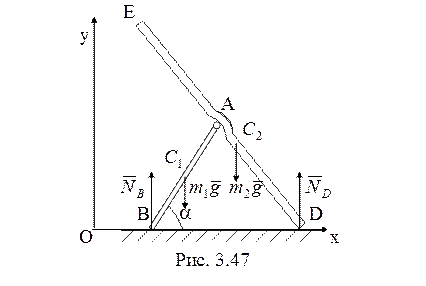 40. В качестве обобщенных координат
рассматриваемой системы с двумя степенями свободы (рис. 3.47) возьмем
координату
40. В качестве обобщенных координат
рассматриваемой системы с двумя степенями свободы (рис. 3.47) возьмем
координату ![]() и угол
и угол ![]() .
Внешние силы тяжести и реакции плоскости вертикальны, составляющая их главного
вектора
.
Внешние силы тяжести и реакции плоскости вертикальны, составляющая их главного
вектора ![]() , и составляющая импульса системы
, и составляющая импульса системы ![]() . Но
. Но ![]() . Так
как
. Так
как 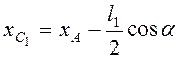 ,
,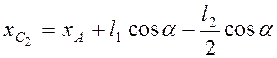 , то составляющие скорости
, то составляющие скорости
 ,
, 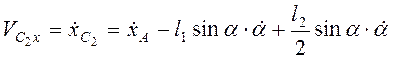 . В момент падения на плоскость угол
. В момент падения на плоскость угол ![]() , и
, и ![]() , т.е.
, т.е. ![]() .
.
Так как работу совершают только консервативные силы тяжести, то выполнен закон сохранения полной механической энергии системы
![]() . (3.63)
. (3.63)
Кинетическая энергия стержней
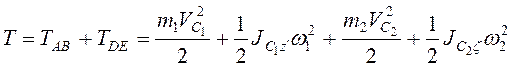 .
.
Координаты центров масс 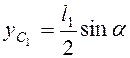 ,
, 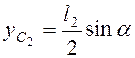 ;
составляющие скорости
;
составляющие скорости
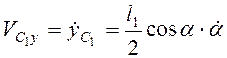 ,
,
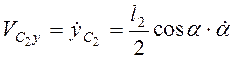 .
. ![]() .
.
Моменты инерции 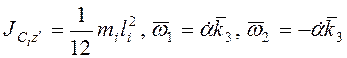 . Поэтому в момент полного соприкосновения
стержней с плоскостью кинетическая энергия системы
. Поэтому в момент полного соприкосновения
стержней с плоскостью кинетическая энергия системы
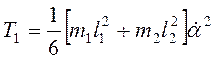 .
.
Потенциальная энергия
системы 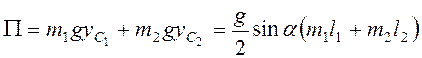 .
.
Подстановка найденных выражений в
(3.63) в момент полного соприкосновения стержней и плоскости даст 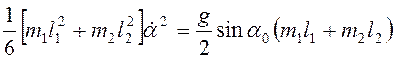 , т.е.
, т.е.
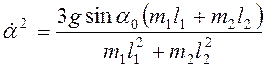 ,
,
и 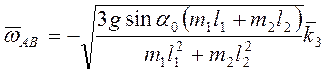 ,
, 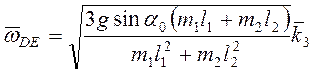 .
.
Ответ: 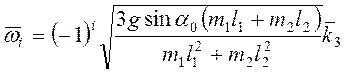 .
.
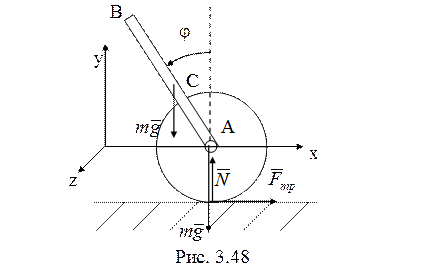 41. В качестве
обобщенных координат рассматриваемой системы с двумя степенями свободы (рис.
3.48) возьмем координату
41. В качестве
обобщенных координат рассматриваемой системы с двумя степенями свободы (рис.
3.48) возьмем координату ![]() и угол
и угол ![]() . Работу при качении без проскальзывания
совершает только консервативная стационарная сила тяжести стержня, и выполнен
закон сохранения полной механической энергии
. Работу при качении без проскальзывания
совершает только консервативная стационарная сила тяжести стержня, и выполнен
закон сохранения полной механической энергии
![]() . (3.64)
. (3.64)
Кинетическая энергия
системы ![]() . Для диска
. Для диска
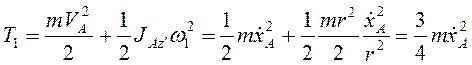 .
.
Для стержня ![]() .
Скорость
.
Скорость ![]() , т.е.
, т.е.
![]() .
.
Момент инерции стержня 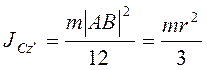 , угловая скорость стержня
, угловая скорость стержня ![]() , и
, и  ,
, 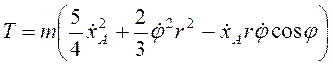 .
.
Потенциальная энергия
системы ![]() . Подстановка найденных выражений в (3.64)
даст
. Подстановка найденных выражений в (3.64)
даст
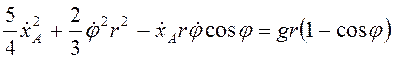 . (3.65)
. (3.65)
Еще один первый интеграл
системы следует из уравнения Лагранжа второго рода по координате ![]() . Действительно
. Действительно 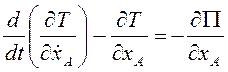 , и
поэтому
, и
поэтому 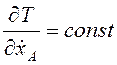 . Так как
. Так как 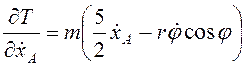 , то с
учетом начальных условий
, то с
учетом начальных условий
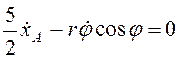 . (3.66)
. (3.66)
В момент удара точки В о
плоскость угол ![]() , и совместное решение уравнений
(3.65) и (3.66) даст для этого момента времени
, и совместное решение уравнений
(3.65) и (3.66) даст для этого момента времени 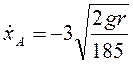 ,
,  . Скорость точки В
. Скорость точки В ![]() .
Для составляющих в момент удара о плоскость
.
Для составляющих в момент удара о плоскость
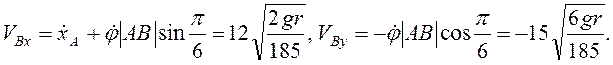
Ответ: 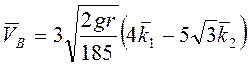 .
.
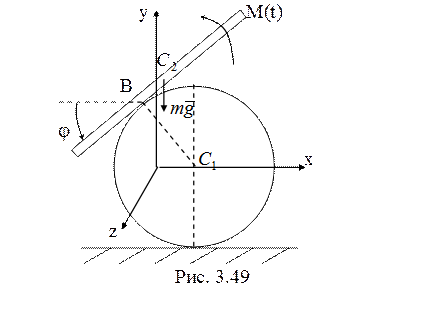 42. Рассматриваемая
система с голономными идеальными связями (рис. 3.49) имеет две степени свободы. В качестве
обобщенных координат возьмем
42. Рассматриваемая
система с голономными идеальными связями (рис. 3.49) имеет две степени свободы. В качестве
обобщенных координат возьмем ![]() . Составим уравнения
Лагранжа второго рода для этой системы
. Составим уравнения
Лагранжа второго рода для этой системы
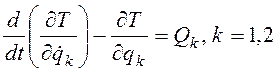 .
.
Кинетическая энергия
системы ![]() . Для цилиндра
. Для цилиндра
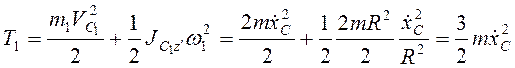 .
.
Для стержня ![]() (при
плоскопараллельном движении). Координаты центра масс стержня
(при
плоскопараллельном движении). Координаты центра масс стержня
![]()
Так как ![]() , то
составляющие скорости
, то
составляющие скорости
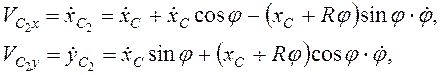
и ![]() .
.
Момент инерции стержня ![]() , угловая скорость
, угловая скорость ![]() ,
и
,
и
![]() .
.
Для всей системы
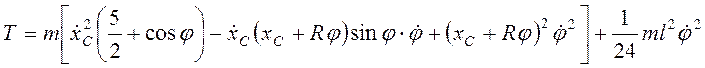 .
.
Виртуальная работа сил, приложенных к системе

Обобщенные силы ![]()
Для составления уравнения
малых колебаний можно подставить полученные выражения в уравнения Лагранжа и
далее провести их линеаризацию в окрестности положения равновесия. Но в этой
задаче более рационально приближенно представить кинетическую энергию системы в
окрестности положения равновесия ![]() с точностью до членов
второго порядка малости по отношению к отклонениям от положения равновесия, а
далее полученное приближенное выражение кинетической энергии подставить в
уравнения Лагранжа. Такие действия эквивалентны их линеаризации. Тогда
с точностью до членов
второго порядка малости по отношению к отклонениям от положения равновесия, а
далее полученное приближенное выражение кинетической энергии подставить в
уравнения Лагранжа. Такие действия эквивалентны их линеаризации. Тогда 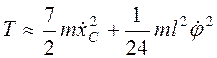 . Обобщенные силы в окрестности положения
равновесия
. Обобщенные силы в окрестности положения
равновесия ![]() ,
, ![]() . Уравнения
малых колебаний принимают вид
. Уравнения
малых колебаний принимают вид
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.