Обработка сигналов и решение систем уравнений

Оглавлнение

1.       Решение нелинейных и алгебраических уравнений. 2

1.1      Решение уравнений вида F(x)=0. 2

1.2      Вычисление корней степенного многочлена. 3

1.3      Функция root в составе функции пользователя. 3

1.4      Решение систем нелинейных уравнений с блоком Given. 3

1.5      Примеры решения нелинейных уравнений.. 5

2    Обработка данных. 7

2.1      Интерполяция, экстраполяция и аппроксимация. 7

2.1.1      Одномерная линейная интерполяция и экстраполяция. 7

2.1.2      Одномерная сплайновая интерполяция и экстраполяция. 7

2.1.3      Примеры линейной и сплайновой интерполяции. 8

2.1.4      Одномерная В-сплайновая интерполяция и экстраполяция. 9

2.1.5      Двумерная линейная и сплайновая интерполяция. 11

2.2      Аппроксимация функций и данных. 11

2.2.1      Приближение функций рядом Тейлора. 11

2.2.2      Интерполяция и экстраполяция функций по Лагранжу. 14

2.2.3      Полиномиальная аппроксимация. 15

2.3      Регрессия. 16

2.3.1      Линейная регрессия. 16

2.3.2      Линейная регрессия общего вида. 18

2.3.3      Одномерная полиномиальная регрессия. 19

2.3.4      Многомерная регрессия. 21

2.3.5      Нелинейная регрессия общего вида. 21

2.3.6      Новые функции для проведения регрессии в Mathcad 2000/2001. 21

2.4      Сглаживание данных. 22

2.4.1      Функции сглаживания данных. 22

2.4.2      Линейное сглаживание по пяти точкам.. 23

2.4.3      Нелинейное сглаживание по семи точкам.. 24

2.4.4      Вейвлет и вейвлет/медианное сглаживание. 25

2.4.5      Комбинированное сглаживание вейвлетами и фильтром «скользящее среднее». 27

2.4.6      Вейвлет-сплайновое сглаживание. 28

2.5      Предсказание зависимостей.. 28

2.5.1      Предсказание методом Бурга «чистых» зависимостей. 28

2.5.2      Предсказание зашумленных зависимостей. 30

2.5.3      Некоторые соображения о прогнозах. 31

1.  Решение нелинейных и алгебраических уравнений

1.1  Решение уравнений вида F(x)=0

Для простейших уравнений вида      F(x)=0 решение находится с помощью функции

 root(Выражение, Имя_переменной).

Эта функция возвращает с заданной точностью значение переменной, при котором выражение равно 0. Функция реализует вычислении итерационным методом, причем перед ее применением надо задать начальное значение переменной. Это особенно полезно, если возможно несколько решений. Тогда выбор одного из них определяется начальным значением переменной. Технику применения функции root для вычисления корней кубического полинома иллюстрирует фрагмент документа Mathcad, показанный на Рис. 1.1

Рис. 1.1 Вычисление корней кубического полинома

Как известно, кубическое уравнение обязательно имеет хотя бы один действительный корень х1. Он найден вначале функцией root. Два других корня могут оказаться как действительными, так и комплексными. Функция root может отыскивать любые корни. Для поиска второго корня х2 первый исключается делением F(x) на (x-x1). Соответственно, для поиска третьего корня x3 нужно повторить деление, при этом F(x) делится еще на (х-х2). Эту процедуру можно распространить и на поиск корней полиномов более высокой степени, однако надо помнить, что найти корни полинома можно гораздо более изящным и простым способом — используя операцию символьных вычислений.

Представленную форму записи функции root поддерживают все версии Mathcad. Однако в последних версиях возможности этой функции расширены, и она может записываться в виде

root(Выражение, Имя_переменной,a,b).

Здесь а и b — границы численного интервала для поиска корней. Такое применение функции root позволяет избежать вывода корней, не представляющих интереса при решении задам, например физических. При этом нет необходимости задавать начальное значение x, поскольку эта переменная определена в заданном интервале [a,b]. Пример:

Примечание. Выражение, корень которого находится функцией rootможет 6ыть представлено в виде F(x) или даже F1(x)-F2(x), если решается уравнение F1(x) = F2(x)

1.2  Вычисление корней степенного многочлена

Рассмотрим обычный полином степени n:

p(x) = a₀+a₁x+a₂x²+...+a_nxⁿ

Для поиска корней этого полинома Mathcad поддерживает очень удобную функцию polyroots(V). Она возвращает вектор всех корней многочлена (полинома) степени n, коэффициенты которого находятся в векторе V, имеющем длину n+1. Системная переменная ORIGIN должна иметь значение 0. Обычно оно задано таким по умолчанию.

Заметим, что корни полинома могут быть как вещественными, так и комплексными числами. Не рекомендуется пользоваться этой функцией, если степень полинома выше пятой-шестой, так как тогда трудно получить малую погрешность вычисления корней. В нижней части фрагмента документа, показанного на Рис. 1.1, имеется пример использования функции для нахождения корней кубического полинома.

1.3  Функция root в составе функции пользователя

Функцию root можно использовать и в составе функции пользователя, что нередко позволяет получать довольно простые решения нетривиальных задач. Примером может служить вычисление функции. Исходные данные и результат решения, представленный в виде вектора G(a,x) и графика, показаны на Рис. 1.2

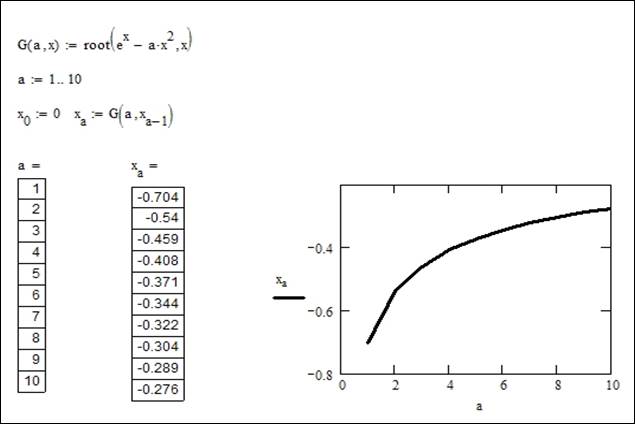
Рис. 1.2 Вычисление функции G(a,x) с помощью функции root в составе функции пользователя

1.4  Решение систем нелинейных уравнений с блоком Given

При решении систем нелинейных уравнений используется специальный вычислительный блок, открываемый директивой             Given и имеющий следующую