23. 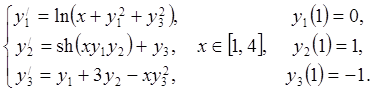
24. 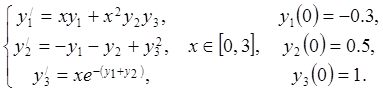
25. 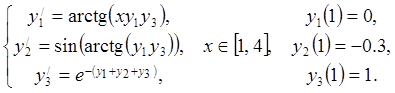
26. 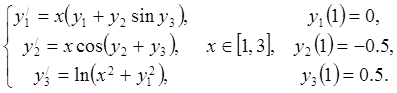
27. 
28. 
29. 
30. 
Дифференциальным уравнением с
частными производными называется уравнение относительно неизвестной функции ![]() двух или более независимых переменных, которое
содержит частные производные этой функции.
двух или более независимых переменных, которое
содержит частные производные этой функции.
Порядком дифференциального уравнения называется наибольший порядок производных, входящих в это уравнение.
Важнейшее значение с точки
зрения приложений в физике и технике имеют уравнения с частными производными
второго порядка, поэтому основное внимание будет уделено изучению именно таких
уравнений. В общем виде дифференциальное уравнение второго порядка относительно
функции двух независимых переменных ![]() записывается следующим
образом:
записывается следующим
образом:
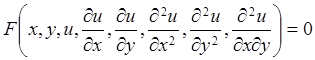 , (8.1.1)
, (8.1.1)
где ![]() -
заданная функция восьми аргументов.
-
заданная функция восьми аргументов.
Далее будут рассматриваться, в основном, уравнения более простого вида, чем (8.1.1), а именно, линейные уравнения второго порядка
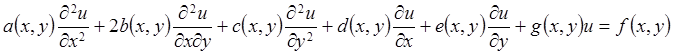 , (8.1.2)
, (8.1.2)
где коэффициенты ![]() и правая часть
и правая часть ![]() -
функции, не зависящие от
-
функции, не зависящие от ![]() , которые заданы и
непрерывны в некоторой области
, которые заданы и
непрерывны в некоторой области ![]() , называемой областью
определения дифференциального уравнения.
, называемой областью
определения дифференциального уравнения.
Если все коэффициенты уравнения (8.1.2) не зависят от ![]() , то оно называется уравнением с
постоянными коэффициентами, если же
, то оно называется уравнением с
постоянными коэффициентами, если же ![]() , уравнение называется однородным.
, уравнение называется однородным.
Естественно возникает вопрос о существовании наиболее компактной формы записи уравнения (8.1.2). Оказывается, этого можно добиться надлежащей заменой переменных. Перепишем уравнение (8.1.2) в следующем виде:
![]() , (8.1.3)
, (8.1.3)
где ![]() . Это уравнение называется линейным
относительно старших производных. Сделаем в нем замену переменных
. Это уравнение называется линейным
относительно старших производных. Сделаем в нем замену переменных ![]() и
и ![]() ,
обеспечивающую взаимно однозначное соответствие между
,
обеспечивающую взаимно однозначное соответствие между ![]() и
и
![]() . Тогда
. Тогда
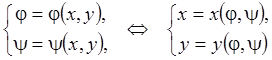 и
и 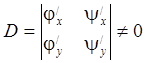 . Так как
. Так как ![]() , то
, то 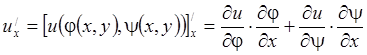 ,
, 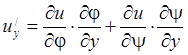 .
Найдем вторую производную по
.
Найдем вторую производную по ![]() , расписав подробно
получающееся выражение:
, расписав подробно
получающееся выражение:
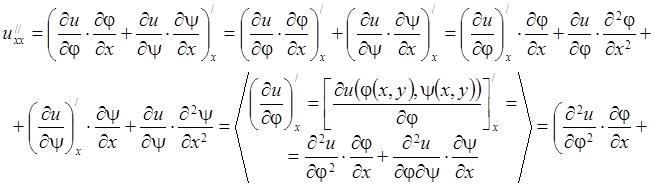
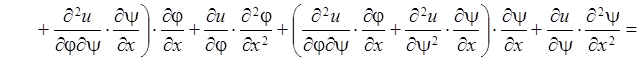
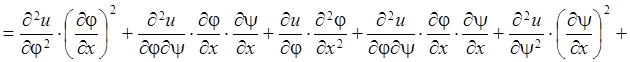
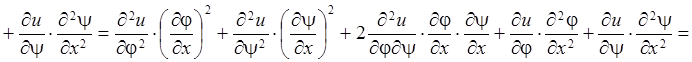
![]()
Аналогично можно записать и ![]() ,
, ![]() .
Подставляя эти значения в уравнение (8.1.3), получим
.
Подставляя эти значения в уравнение (8.1.3), получим
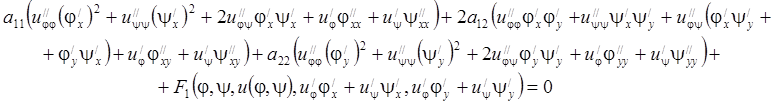
или ![]() где
где
![]() , а
, а
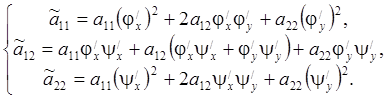
Естественно, для упрощения уравнения ![]() в
новых переменных
в
новых переменных ![]() и
и ![]() надо
так подобрать эти переменные, чтобы хотя бы некоторые члены рассматриваемого
уравнения упрощались или вообще обнулялись. Например, можно выбрать
надо
так подобрать эти переменные, чтобы хотя бы некоторые члены рассматриваемого
уравнения упрощались или вообще обнулялись. Например, можно выбрать ![]() и
и ![]() так,
чтобы
так,
чтобы ![]() . Для этого рассмотрим вспомогательное
уравнение
. Для этого рассмотрим вспомогательное
уравнение ![]() , где
, где ![]() . Пусть
. Пусть ![]() - какое-нибудь частное решение этого
уравнения. Если теперь выбрать
- какое-нибудь частное решение этого
уравнения. Если теперь выбрать ![]() , то
, то ![]() . Аналогично, если
. Аналогично, если ![]() - другое частное решение этого же уравнения и
- другое частное решение этого же уравнения и ![]() , то
, то ![]() .
.
Теорема 8.1.
Если ![]() является частным решением уравнения
является частным решением уравнения ![]() , то
, то ![]() есть
общий интеграл обыкновенного дифференциального уравнения
есть
общий интеграл обыкновенного дифференциального уравнения
![]() . (8.1.4)
. (8.1.4)
Наоборот, если ![]() - общий интеграл
обыкновенного дифференциаль-
- общий интеграл
обыкновенного дифференциаль-
ного уравнения (8.1.4), то функция ![]() удовлетворяет уравнению
удовлетворяет уравнению
![]() .
.
Решим уравнение (8.1.4), преобразовав его: 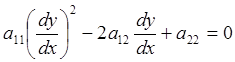 ,
, 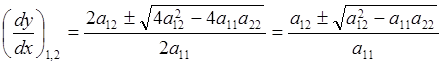 .
Таким образом, получим два обыкновенных дифференциальных уравнения:
.
Таким образом, получим два обыкновенных дифференциальных уравнения:
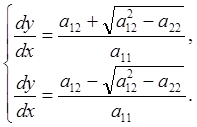 (8.1.5)
(8.1.5)
Знак подкоренного выражения определяет тип исходного уравнения (8.1.3) в частных производных.
1. Если в точке ![]()
![]() ,
то уравнение
,
то уравнение ![]() в этой точке называется
уравнением гиперболического типа.
в этой точке называется
уравнением гиперболического типа.
2. Если в точке ![]()
![]() ,
то уравнение
,
то уравнение ![]() в этой точке называется
уравнением эллиптического типа.
в этой точке называется
уравнением эллиптического типа.
3. Если в точке ![]()
![]() ,
то уравнение
,
то уравнение ![]() в этой точке называется
уравнением параболического типа.
в этой точке называется
уравнением параболического типа.
Так как ![]() , то сказанное
справедливо и для уравнения
, то сказанное
справедливо и для уравнения ![]() .
.
Уравнение (8.1.4) называется характеристическим для
уравнения (8.1.3), а интегралы уравнения (8.1.4) - характеристиками уравнения
(8.1.3). Пусть в заданной области ![]() уравнение (8.1.3)
однотипно. Рассмотрим все три возможные случая подробнее.
уравнение (8.1.3)
однотипно. Рассмотрим все три возможные случая подробнее.
1. Гиперболический тип.
Два общих интеграла уравнения (8.1.3) ![]() и
и ![]() определяют действительные семейства
характеристик. Пусть
определяют действительные семейства
характеристик. Пусть ![]() и
и ![]() - новые переменные в уравнении
(8.1.3). Тогда
- новые переменные в уравнении
(8.1.3). Тогда ![]() или
или ![]() -
первая каноническая форма уравнения гиперболического типа. Если положить
-
первая каноническая форма уравнения гиперболического типа. Если положить 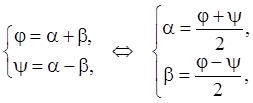 то
то 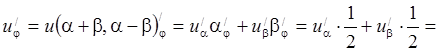
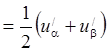 . Аналогично,
. Аналогично, 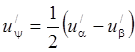 и
и 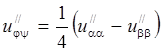 . В результате исходное уравнение примет
вид
. В результате исходное уравнение примет
вид ![]() . Это вторая каноническая форма уравнения
гиперболического типа.
. Это вторая каноническая форма уравнения
гиперболического типа.
2. Параболический тип.
Для уравнения этого типа ![]() , имеется, следовательно,
лишь один общий интеграл характеристического уравнения
, имеется, следовательно,
лишь один общий интеграл характеристического уравнения ![]() . Пусть этот интеграл
. Пусть этот интеграл ![]() , положим
, положим ![]() ,
,
![]() , где
, где ![]() - любая
функция, не зависящая от
- любая
функция, не зависящая от ![]() . Тогда
. Тогда ![]() , потому что при
, потому что при ![]()
![]() . Далее
. Далее ![]()
![]() . Тогда исходное для этого случая уравнение
. Тогда исходное для этого случая уравнение
![]() обратится в следующее:
обратится в следующее: ![]() . Это канонический вид уравнения
параболического типа.
. Это канонический вид уравнения
параболического типа.
3. Эллиптический тип. Для этого
типа уравнения 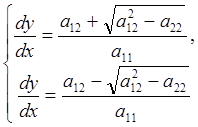 имеют комплексные общие
интегралы. По свойству комплексной переменной, если
имеют комплексные общие
интегралы. По свойству комплексной переменной, если ![]() -
решение уравнения
-
решение уравнения ![]() , то
, то ![]() - комплексно-сопряженная функция также
будет решением этого уравнения. Пусть
- комплексно-сопряженная функция также
будет решением этого уравнения. Пусть ![]() ,
, ![]() , тогда уравнение эллиптического типа
сведется к тому же виду, что и гиперболическое. Чтобы не иметь дело с
комплексными переменными, введем новые переменные
, тогда уравнение эллиптического типа
сведется к тому же виду, что и гиперболическое. Чтобы не иметь дело с
комплексными переменными, введем новые переменные 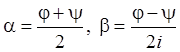 ,
тогда
,
тогда ![]() . При этом предполагается, что
. При этом предполагается, что ![]() - аналитические функции.
- аналитические функции.
Вычислим ![]()
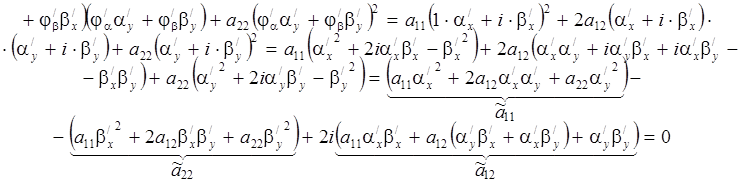
Отсюда по свойству комплексных чисел следует, что ![]() , так как
, так как ![]() . Тогда
уравнение
. Тогда
уравнение ![]() превратится в следующее уравнение:
превратится в следующее уравнение: ![]() или
или 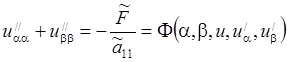 -
канонический вид уравнения эллиптического типа.
-
канонический вид уравнения эллиптического типа.
Итак: 1) ![]() -
гиперболический тип и
-
гиперболический тип и ![]() или
или ![]() - канонический
вид уравнения;
- канонический
вид уравнения;
2) ![]() - эллиптический
тип, а
- эллиптический
тип, а ![]() - канонический вид уравнения;
- канонический вид уравнения;
3) ![]() - параболический
тип и
- параболический
тип и ![]() - канонический вид
уравнения.
- канонический вид
уравнения.
Пример. Найти области гиперболичности, эллиптичности
и параболичности уравнения ![]() и привести его к
каноническому виду в области гиперболичности.
и привести его к
каноническому виду в области гиперболичности.
Дифференциальное уравнение в частных производных, содержащее
явно все необходимые коэффициенты, имеет вид ![]() . В
нашем случае
. В
нашем случае ![]() , то есть
, то есть ![]() .
Тип уравнения зависит от знака выражения
.
Тип уравнения зависит от знака выражения ![]() . Если
оно отрицательно, то это эллиптический тип, положительно - гиперболический,
равно нулю – параболический:
. Если
оно отрицательно, то это эллиптический тип, положительно - гиперболический,
равно нулю – параболический:
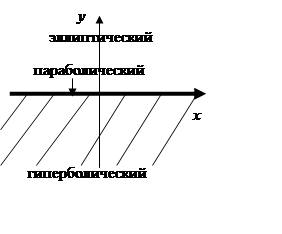 1)
1) ![]() - область гиперболического типа;
- область гиперболического типа;
2) ![]() - область эллиптического типа;
- область эллиптического типа;
3) ![]() - область параболического типа.
- область параболического типа.
Все области изображены на рисунке слева. Приведем теперь исходное уравнение к каноническому виду. Для этого решим уравнения (8.1.5):
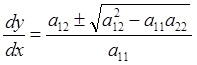 ,
,
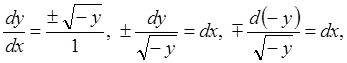
![]() . Итак,
. Итак, 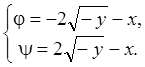
![]()
Пример. Привести к каноническому виду следующее
дифференциальное уравнение 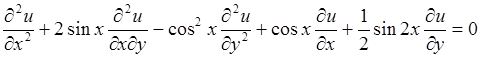 .
.
Здесь ![]() . Составим и решим
характеристическое уравнение:
. Составим и решим
характеристическое уравнение: 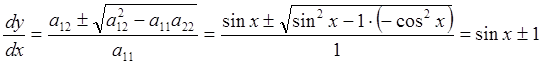 .
Отсюда
.
Отсюда ![]() , то есть два первых интеграла
характеристического уравнения имеют вид
, то есть два первых интеграла
характеристического уравнения имеют вид 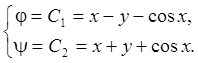 Обратное
преобразование, нужное для нахождения производных
Обратное
преобразование, нужное для нахождения производных ![]() ,
вычисления
,
вычисления ![]() и
и ![]() , также
легко находится:
, также
легко находится: ![]()
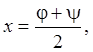
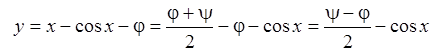 . Так как
. Так как ![]() , то
исходное уравнение – уравнение гиперболического типа. Его первая каноническая
форма
, то
исходное уравнение – уравнение гиперболического типа. Его первая каноническая
форма 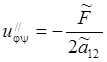 , где
, где ![]() ,
, ![]() , а
, а ![]() определяется
из исходного уравнения
определяется
из исходного уравнения ![]() . В нашем случае
. В нашем случае 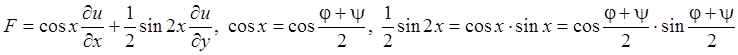 . Далее вычисляем необходимые производные:
. Далее вычисляем необходимые производные: 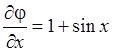 ,
, 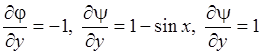 ,
, 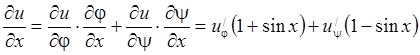 ,
, 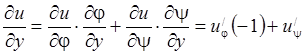 .
Тогда
.
Тогда 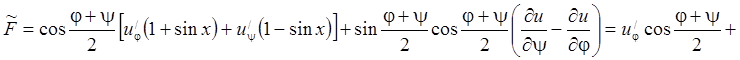
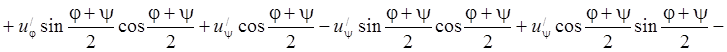
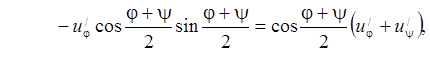
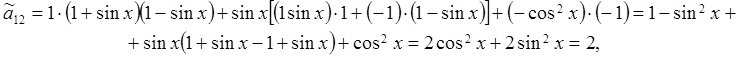
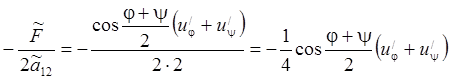 . Тогда, окончательно, канонический
вид исходного уравнения второго примера будет таким
. Тогда, окончательно, канонический
вид исходного уравнения второго примера будет таким 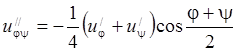 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.