Свойства разностных схем для дифференциальных уравнений: способность аппроксимировать исходную дифференциальную задачу, устойчивость и сходимость

8.7. Свойства разностных схем для дифференциальных уравнений: способность аппроксимировать исходную дифференциальную задачу, устойчивость и сходимость

Общая схема решения задач для дифференциальных уравнений методом конечных разностей, которая была использована выше, состоит в следующем. Пусть задан некоторый дифференциальный оператор второго порядка , который является линейным, то есть обладает свойством , справедливым для любых дважды непрерывно дифференцируемых функций ,  и действительных чисел , . Для решения уравнения

                                                                     (8.7.1)

в области его определения  вводится прямоугольная вычислительная сетка и дифференциальный оператор  аппроксимируется конечно-разностным оператором , так что для точного решения , гарантированного теоремой существования, справедливо равенство , где - погрешность аппроксимации. Если погрешность  стремится к нулю при неограниченном измельчении сетки, то говорят, что разностная схема удовлетворяет свойству аппроксимации дифференциального оператора. В разностных схемах,
использованных в подразд. 8.4 – 8.6, погрешность имела вид  или .

В результате исходное дифференциальное уравнение может быть переписано так

,                                                      (8.7.2)

в узлах сетки, где . Опуская погрешность, получаем систему алгебраических уравнений

                                                              (8.7.3)

относительно приближенного решения .

Для оценки точности приближенного решения важное значение имеет свойство устойчивости решения системы уравнений (8.7.3), которое состоит в следующем. Пусть - некоторое возмущение правой части системы и  - соответствующее ему решение системы

.                                                   (8.7.4)

Вычитая (8.7.3) из (8.7.4), получаем . В силу линейности оператора  отсюда находим . Свойство устойчивости записывается в виде

 или ,                                       (8.7.5)

где  - выбранные нормы в конечномерных пространствах, которым принадлежат искомое решение и правая часть системы, а постоянная  не зависит от  и зависит только от коэффициентов оператора . Устойчивость решения означает малые его изменения при малых изменениях правой части системы. Покажем, что свойства аппроксимации и устойчивости обеспечивают сходимость приближенного решения к точному: аппроксимация + устойчивость => сходимость.

Действительно, для разности  где  - значения решения уравнения (8.7.1) в узлах сетки, а  - решение системы (8.7.3), благодаря свойству устойчивости (8.7.5) получаем

.

Теперь, добавляя и вычитая в правой части , преобразуем ее следующим образом:

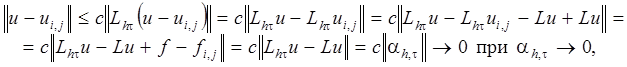
так как  в узлах сетки.

8.8. Некоторые обобщения

Линейные уравнения параболического, гиперболического и эллиптического типов с переменными коэффициентами согласно (8.3.1), (8.3.4), (8.3.6) имеют вид

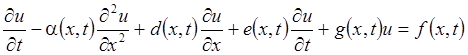,                           (8.8.1)

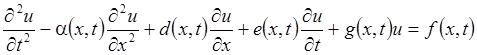,                            (8.8.2)

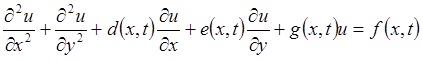,                               (8.8.3)

где . Решение краевых задач для уравнений (8.8.1) – (8.8.3) может осуществляться с помощью тех же разностных схем, которые описаны в подразд. 8.4 – 8.6, хотя в некоторых случаях могут возникать определенные трудности, например, в случае уравнения параболического типа (8.8.1) с преобладающем влиянием конвективного слагаемого 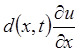 по сравнению с диффузионным слагаемым  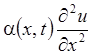(см. (8.4.20)). Отметим также важное отличие уравнения эллиптического типа (8.8.3) от первых двух, состоящее в необходимости выполнения условия  в области , которое обеспечивает существование и единственность точного решения краевой задачи. При нарушении этого условия корректность исходной задачи может нарушаться.

В качестве краевых условий могут быть заданы не значения решения на границе рассматриваемой области, а значения его производной по нормали к границе. Например, для уравнения (8.8.1) может быть рассмотрена задача в прямоугольнике 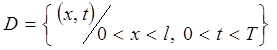 с начальными условиями (8.3.2) и краевыми условиями

,

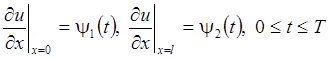которые заменяют условия (8.3.3). Решение такой задачи может быть получено с помощью тех же разностных схем, которые построены в подразд. 8.4. Действительно, значение приближенного решения во внутренних узлах  слоя  может быть найдено, например, по формуле (8.4.9). Значения решения в левой граничной точке  могут быть получены из соотношения для трехточечной аппроксимации первой производной: 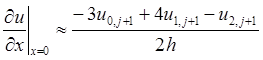, погрешность которой имеет порядок . Аналогично, значения решения в правой граничной точке  могут быть найдены из соотношения 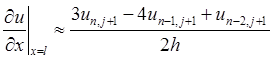. Поэтому значения приближенного решения во всех узлах, расположенных на слое , оказываются известными, и можно переходить к нахождению решения на слое .

Примерами нелинейных уравнений параболического, гиперболического