














Решить задачу Коши для дифференциального уравнения первого порядка методом Эйлера. При ручном счете сделать три шага с шагом интегрирования h = 0.1. При машинном счете решить уравнение с количеством шагов n = 10. Построить интегральную кривую уравнения.
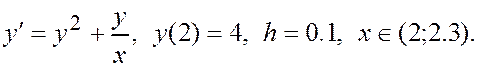
ЗАДАНИЕ III.
Решить задачу Коши для системы дифференциальных уравнений первого порядка методом Эйлера. При ручном счете сделать три шага с шагом интегрирования h = 0.1. При машинном счете решить уравнение с количеством шагов n = 10. Построить интегральные кривые системы уравнений.
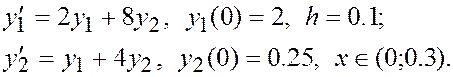
ЗАДАНИЕ IV.
Решить задачу Коши для дифференциального уравнения второго порядка методом Эйлера. При ручном счете сделать три шага с шагом интегрирования h = 0.1. При машинном счете решить уравнение с количеством шагов n = 10. Построить интегральную кривую уравнения.
![]()
ЗАДАНИЕ V. (Курсовой проект)
1. Записать конечно-разностную систему уравнений решения краевой задачи для линейного дифференциального уравнения второго порядка.
![]()
Вариант 2.
ЗАДАНИЕ I.
Решить методом прогонки системы линейных уравнений с трехдиагональной матрицей. Сделать проверку решения, подставив найденные значения неизвестных во все уравнения системы.
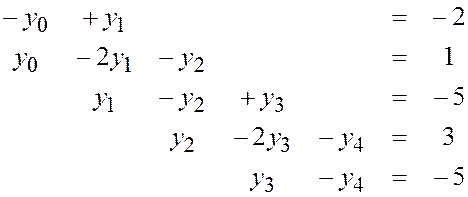
ЗАДАНИЕ II.
Решить задачу Коши для дифференциального уравнения первого порядка методом Эйлера. При ручном счете сделать три шага с шагом интегрирования h = 0.1. При машинном счете решить уравнение с количеством шагов n = 10. Построить интегральную кривую уравнения.
![]()
ЗАДАНИЕ III.
Решить задачу Коши для системы дифференциальных уравнений первого порядка методом Эйлера. При ручном счете сделать три шага с шагом интегрирования h = 0.1. При машинном счете решить уравнение с количеством шагов n = 10. Построить интегральные кривые системы уравнений.
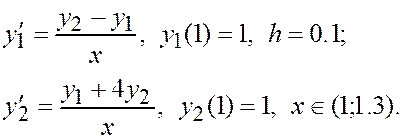
ЗАДАНИЕ IV.
Решить задачу Коши для дифференциального уравнения второго порядка методом Эйлера. При ручном счете сделать три шага с шагом интегрирования h = 0.1. При машинном счете решить уравнение с количеством шагов n = 10. Построить интегральную кривую уравнения.
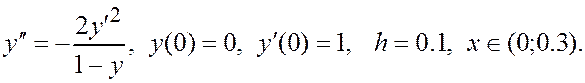
ЗАДАНИЕ V. (Курсовой проект)
1. Записать конечно-разностную систему уравнений решения краевой задачи для линейного дифференциального уравнения второго порядка.
![]()
Вариант 3.
ЗАДАНИЕ I.
Решить методом прогонки системы линейных уравнений с трехдиагональной матрицей. Сделать проверку решения, подставив найденные значения неизвестных во все уравнения системы.
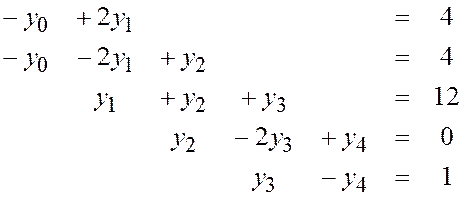
ЗАДАНИЕ II.
Решить задачу Коши для дифференциального уравнения первого порядка методом Эйлера. При ручном счете сделать три шага с шагом интегрирования h = 0.1. При машинном счете решить уравнение с количеством шагов n = 10. Построить интегральную кривую уравнения.
![]()
ЗАДАНИЕ III.
Решить задачу Коши для системы дифференциальных уравнений первого порядка методом Эйлера. При ручном счете сделать три шага с шагом интегрирования h = 0.1. При машинном счете решить уравнение с количеством шагов n = 10. Построить интегральные кривые системы уравнений.
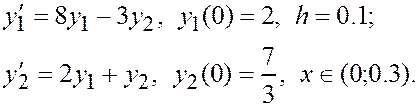
ЗАДАНИЕ IV.
Решить задачу Коши для дифференциального уравнения второго порядка методом Эйлера. При ручном счете сделать три шага с шагом интегрирования h = 0.1. При машинном счете решить уравнение с количеством шагов n = 10. Построить интегральную кривую уравнения.
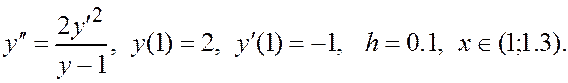
ЗАДАНИЕ V. (Курсовой проект)
1. Записать конечно-разностную систему уравнений решения краевой задачи для линейного дифференциального уравнения второго порядка.
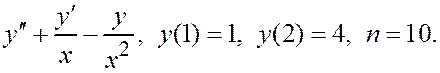
Вариант 4.
ЗАДАНИЕ I.
Решить методом прогонки системы линейных уравнений с трехдиагональной матрицей. Сделать проверку решения, подставив найденные значения неизвестных во все уравнения системы.
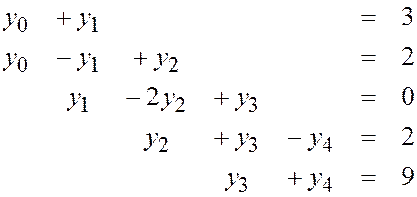
ЗАДАНИЕ II.
Решить задачу Коши для дифференциального уравнения первого порядка методом Эйлера. При ручном счете сделать три шага с шагом интегрирования h = 0.1. При машинном счете решить уравнение с количеством шагов n = 10. Построить интегральную кривую уравнения.
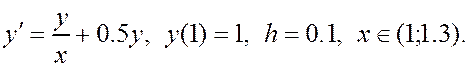
ЗАДАНИЕ III.
Решить задачу Коши для системы дифференциальных уравнений первого порядка методом Эйлера. При ручном счете сделать три шага с шагом интегрирования h = 0.1. При машинном счете решить уравнение с количеством шагов n = 10. Построить интегральные кривые системы уравнений.
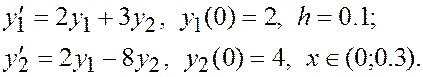
ЗАДАНИЕ IV.
Решить задачу Коши для дифференциального уравнения второго порядка методом Эйлера. При ручном счете сделать три шага с шагом интегрирования
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.