Решение уравнения с помощью методов дихотомии, хорд, Ньютона в MSExcel и в VisualBasic

Министерство образования и науки Российской Федерации

Санкт-Петербургский Государственный архитектурно-строительный университет

кафедра прикладной математики и информатики

КУРСОВАЯ РАБОТА

по информатике и ИКТ

 по теме

«Решение уравнения x3-2,56x²-1,3251x+4,395006=0 с помощью методов дихотомии, хорд, Ньютона в MSExcel и в VisualBasic»

Работу выполнила студентка

1 курса группы 1-РРАН-I

строительного института

специальности «Реставрация и

реконструкция архитектурного

наследия» Богданова М. А.

Работу проверила ассистент

Григорьева Ксения Владимировна

Санкт-Петербург

2005

Содержание

Метод деления отрезка пополам.. 3

Метод хорд. 3

Приближенное решение уравнений методом касательных. 4

Метод Ньютона. 4

Решение уравнения методом деления отрезка пополам в MS Excel. 5

Решение уравнения методом хорд в MS Excel. 7

Решение уравнения методом Ньютона  в MS Excel. 8

User Form по решению уравнения x³+2,56*x²-1,3251*x+4,395006=0 указанными методами.. 9

литература………………………………………………………..11

Метод деления отрезка пополам

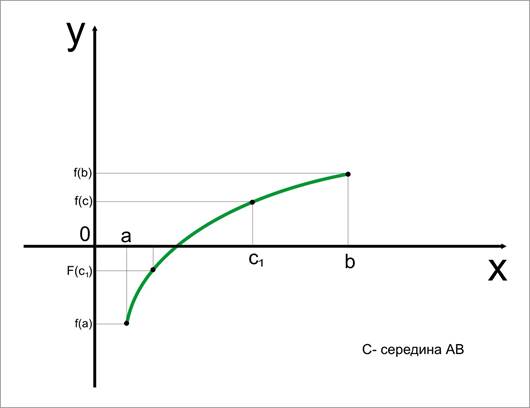
Пустьf(x) непрерывна на концах отрезка [a;b] имеет разные знаки, т.е. f(a)*f(b)<0, тогда f(x)=0 на данном отрезке будет иметь единственные корень. Отрезок [а;b] называется отрезком локализации этого корня.

Пусть с=(a+b)/2, середина отрезка [а;b]. Если f(a)*f(b)<=0, то корень на отрезке от [а;с], иначе корень на отрезке от [а;b]

Новый отрезок локализации в 2 раза меньше первоначального. Процесс деления отрезка для локализации корня продолжаем до тех пор пока его длина не станет < Е, где Е- точность нахождения корня. В этом случае любая точка отрезка локализации отлична от коня не более чем на Е/2.

Метод хорд.

 Пустьf(x) непрерывна на концах отрезка [a;b] имеет разные знаки. Также для функции выполняются следующие условия:

непрерывна и дифференцируема на [a;b]

f(x), f’(x), f’’(x) на концах [a;b]

f’(x), f’’(x) на (a;b) сохраняет знак

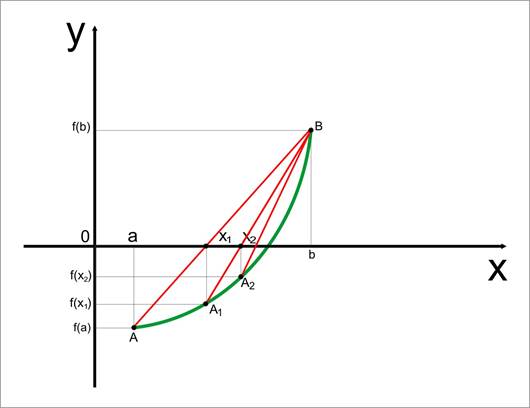
Процесс вычисления корня уравнения f(x)=0 на отрезке[a;b] состоит из следующих этапов:

Пусть f(a)<0,  f(b)>0

Точка A(a;f(a)) и B(b;f(b)) соединим хордой. За исходное приближенное значение исходного корня примем абсциссу х₁ – точка пересечения АВ с осью x

По формуле

х₁ = а-(b-a)*f(a)/f(b)-f(a), где х₁є(a;b)

Пусть f(х₁)<0, следовательно более узкий отрезок изоляции примем отрезок от [х₁;b]

Получим в точке пересечения хорды а₁и с О_х второе приближенное значение х₂, которое вычислим по формуле

 х₂ = х₁-(b- х₁)*f(х₁)/f(b)-f(х₁)

Последовательность чисел а, х₁, х₂… стремится к искомому корню уравнения. Процесс вычисления корней уравнения продолжается до тех пор, пока его длина не станет <= Е, т.е. точности нахождения корня.

Приближенное решение уравнений методом касательных.

Метод Ньютона.

Пустьf(x) непрерывна на концах отрезка [a;b] имеет разные знаки.

Предположим, что все условия для отрезка от [a;b], рассматриваемые в предыдущих методах, справедливы и в данном случае.

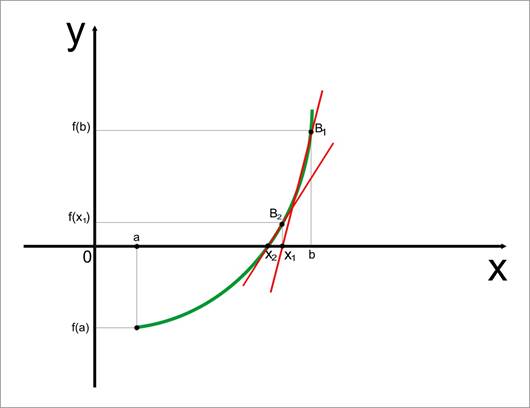
Для определенности проведем касательную к точке В₁ (b;f(x)). Эта касательная пересекает ось х в точке  х₁.

Проведем касательную через точку В₂ (х₁;f(х₁))

Проведем касательную через точку В₃ (х₂;f(х₂))

Этот процесс будет продолжаться пока (x_i-1-x_i)<= Е

Применяем уравнение касательной х₁=х₀-f(x₀)/f’(x₀)

х₂=x₁-f(х₁)/f’(х₁)

X_i+1=x_i-f(x_i)/f’(x_i)

Решение уравнения методом деления отрезка пополам MS Excel

Мы имеем уравнение третьего порядка, следовательно, мы получим в этом уравнение три корня. Для того чтобы решить уравнение методом дихотомии мы должны первоначально корни локализовать, т.е. найти интервалы на которых эти корни  существуют. Такими интервалами локализации корней могут служить промежутки, на концах которых функция имеет противоположный знак. Чтобы найти эти промежутки необходимо либо построить график функции, либо ее протабулировать.

Проделаем эти два способа:

x	y	0,5	3,21746
-2	-11,195	0,6	2,89435
-1,9	-9,1879	0,7	2,55604
-1,8	-7,3462	0,8	2,20853
-1,7	-5,6637	0,9	1,85782
-1,6	-4,1344	1	1,50991
-1,5	-2,7523	1,1	1,1708
-1,4	-1,5115	1,2	0,84649
-1,3	-0,4058	1,3	0,54298
-1,2	0,57073	1,4	0,26627
-1,1	1,42402	1,5	0,02236
-1	2,16011	1,6	-0,1828
-0,9	2,785	1,7	-0,3431
-0,8	3,30469	1,8	-0,4526
-0,7	3,72518	1,9	-0,5053
-0,6	4,05247	2	-0,4952
-0,5	4,29256	2,1	-0,4163
-0,4	4,45145	2,2	-0,2626
-0,3	4,53514	2,3	-0,0281
-0,2	4,54963	2,4	0,29317
-0,1	4,50092	2,5	0,70726
0	4,39501	2,6	1,22015
0,1	4,2379	2,7	1,83784
0,2	4,03559	2,8	2,56633
0,3	3,79408	2,9	3,41162
0,4	3,51937	3	4,37971