Линейные алгебраические преобразования и матричные операции в среде Microsoft Excel (Лабораторная работа № 1)

Лабораторная работа № 1

Линейные алгебраические преобразования и матричные операции в среде Microsoft Excel

Мастер функций, реализованный в среде программы Microsoft Excel, содержит функции, обеспечивающие преобразования и математические операции над скалярными, векторными и матричными объектами. В этой лабораторной работе рассматриваются методики, используемые при выполнения векторных и матричных операций.

В категорию математических функций, открываемую при выполнении второго шага мастера функций программы Excel, включены такие функции, как:

a.  МОБР - возвращает обратную матрицу (матрица хранится в массиве);

b.  МОПРЕД - вычисляет определитель матрицы (матрица хранится в массиве);

c.  МУМНОЖ - возвращает произведение матриц (матрицы хранятся в массиве);

d.  СУММ – суммирует аргументы функции. Суммируемые числа могут быть записаны в массив ячеек таблицы;

e.  СУММЕСЛИ - суммирует числа в ячейках, специфицированных заданным критерием;

f.  СУММКВ – возвращает сумму квадратов аргументов. Аргументами могут быть числа, массивы, имена или ссылки на ячейки, содержащие числа;

g.  СУММКВРАЗН – возвращает сумму квадратов разностей числовых значений, записанных в соответствующие ячейки двух массивов;

h.  СУММПРОИЗВ - возвращает сумму произведений числовых значений, записанных в соответствующие ячейки двух массивов;

a.  СУММРАЗНКВ – возвращает сумму разностей квадратов числовых значений, записанных в соответствующие ячейки двух массивов;

b.  СУММСУММКВ - возвращает сумму сумм квадратов значений, записанных в соответствующие ячейки двух массивов.

В категорию статистических функций входит большое число функций, обеспечивающих вычисление различных статистических характеристик для векторных и матричных наборов данных. Наиболее часто при решении задач обработки данных используются такие функции как:

-  функции для оценки различных видов дисперсии по выборке случайных чисел ДИСП, ДИСПА, ДИСПР, ДИСПРА;

-  функции для оценки средних значений выборки случайных чисел СРЗНАЧ, СРГАРМ, СРГЕОМ, СРОТКЛ и др.;

Пример выполнения лабораторной работы

"Обработка массивов и решение систем линейных алгебраических уравнений"

Задание 1

Решить системы линейных уравнений         A*X₁ = B, и A³*X₂ = B где матрица А=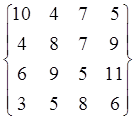 и вектор В=.

1а) Решение системы линейных алгебраических уравнений A*X₁ = B может быть получено по формуле Х=А^-1*В.

Для вычисления значения обратной матрицы А^-1  выделяем массив ячеек A11:D14. В ячейку А11 записываем формулу =МОБР(A6:D9) после чего одновременным нажатием клавиш Ctrl + Shift + Enter в выделенные ячейки таблицы заносятся значения элементов обратной матрицы А^-1.

Для вектора решения первой системы линейных уравнений выделяем ячейки F11:F14. После чего в ячейку F11 вводим формулу =МУМНОЖ(A11:D14;F6:F9) и для выполнения решения нажимаем клавиши Ctrl + Shift + Enter.

Проверка правильности полученного решения обеспечивается перемножением исходной матрицы А на полученный в решении вектор Х в результате чего должен быть получен вектор, значения элементов которого должны совпадать со значениями, соответствующими значениям элементов вектора В.

 

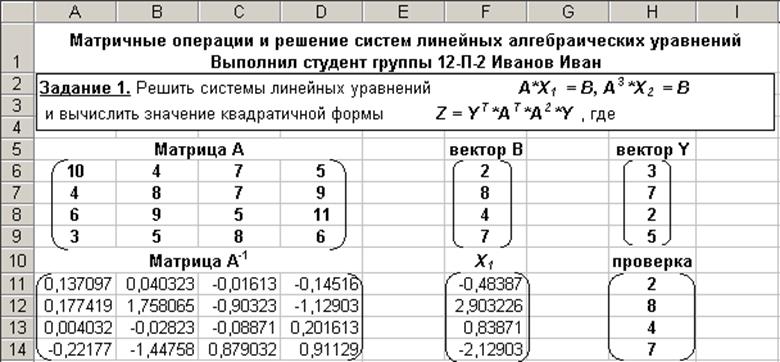Рис. 1. Результаты выполнения задания 1а

1б) Решение системы линейных алгебраических уравнений A³*X₂ = B для тех же значений матрицы А и вектора В.

Для решения этой системы необходимо сначала вычислить значения элементов матриц A² и A³. Эти матрицы вычисляются последовательным умножением матрицы А на самоё себя, а затем ещё одним перемножением матрицы A² на А. После чего вычисляются элементы матрицы обратной матрице A³ и находится вектор решения X₂ = (A³)^-1.

 

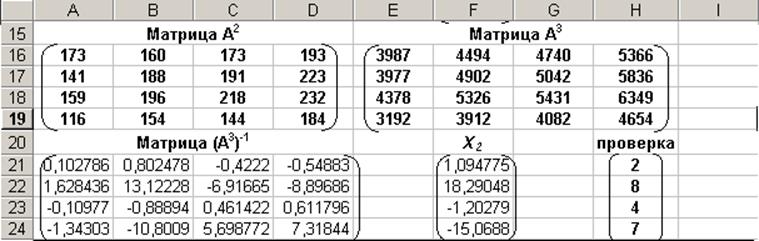Рис.2. Алгоритм выполнения второго шага задания: решение системы A³*X₂ = B

Задание 2

Вычислить массив значений, элементы которого определяются формулой

 

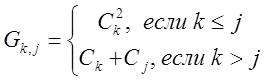где C - вектор, содержащий n элементов.

На рис. 3 показан результат выполнения этого задания для вектора С={4, 3, 7}.

 

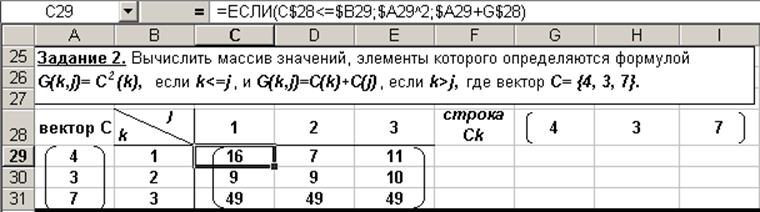Рис. 3. Результаты выполнения второго задания

При выполнении этого задания особое внимание следует обратить на правильность индексации элементов вектора C, входящих в формулу.

В предлагаемом варианте решения вектор С реализован в двух вариантах: как вектор-столбец в ячейках А29:А31 и как вектор-строка в ячейках G28:I28.

Индекс строки k, определяется в ячейках B29:B31, а индекс j - в ячейках С28:E28. Для вычисления значения G(k,j) в ячейку C29 записываем формулу

=ЕСЛИ(C$28<=$B29;$A29^2;$A29+G$28)

После чего протягиваем эту формулу до ячейки Е31. Окончательный результат приведён на рис. 3.

Задание 3

Вычислить значение функции S, представляемой формулой

 

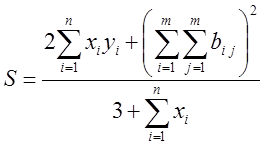где X и Y - векторы размерности n=4, а B - матрица размерности m=2.

Результат выполнения этого задания показан на рис. 4.

 

Рис. 4. Решение задачи вычисления функции S

В ячейку G40 записываем формулу   =СУММ(A41:A44*B41:B44),

обеспечивающую вычисление суммы 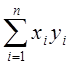. В ячейку G42 записываем формулу =СУММ(C41:D42), обеспечивающую вычисление суммы элементов массива b, а в ячейку G44 формулу =СУММ(A41:A44) для вычисления суммы элементов вектора Х. В ячейку I42 введём формулу

=(2*G40+G42^2)/(3+G44)

Эта формула реализует окончательное вычисление суммы S.