












групповом поле Type включаем кнопку переключателя Function.
Назовём создаваемую нами функцию Fsin.
В окне редактора Visual Basic открывается заготовка текста создаваемой функции, которую мы дополним необходимыми операторами. Окончательно текст этой функции будет иметь следующий вид:
Public Function Fsin(a, b, x)
Fsin = 5 * Sin(x + a) - b * x ^ 2
End Function
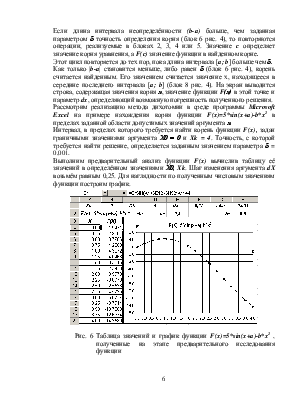
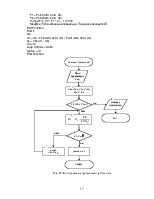
Создадим таблицу для уточнения корня уравнения F(x)=5*sin(x+a)-b*x2 в выделенном интервале [2,00; 2,25]. Формат её заголовка показан на рис. 7.

Рис.7. Заголовок таблицы для реализации алгоритма метода дихотомии
В ячейки 25-й строки записываются формулы, обеспечивающие формирование первой строки таблицы, в которой будет реализован метод дихотомии. Так в ячейку А25 записывается формула "=В23" - ссылка на ячейку, в которой записано значение аргумента Х0, соответствующее левой границе выделенного интервала неопределённости. В ячейку В25 записывается формула "=D23" - ссылка на ячейку, в которую записано значение правой границы выделенного интервала неопределённости.
В ячейку С25 записывается формула, по которой вычисляется значение аргумента Х, определяющее срединную точку интервала неопределённости:
=(А25+В25)/2
Формула, по которой вычисляется значение функции F(x) в точке а, определяющей левую границу выделенного интервала неопределённости записывается в ячейку D25.
Обращение к функции Fsin выполняется через мастер функций программыMicrosoft Excel. ФункцияFsin выбирается из категории функций определённых пользователем.
На рис. 8 показано окно второго шага мастера функций, вызываемого при формировании обращения к функции Fsin.
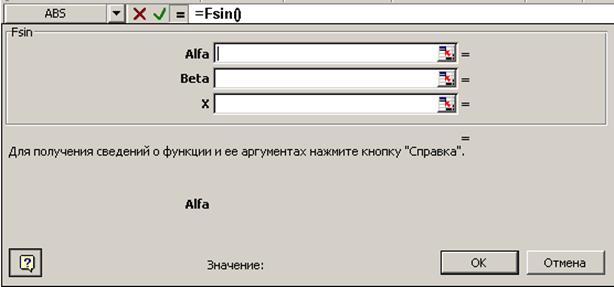 |
Рис. 8. Окно второго шага мастера функций для функции Fsin()
В поле ввода Alfa этого окна записывается абсолютная ссылка $E$22 на ячейку Е22, в которую записано значение параметра функции a.
В поле ввода Beta записывается абсолютная ссылка $H$22 на ячейку H22, хранящую значение параметра функции b. В поле ввода X записывается относительная ссылкаA25 на ячейку таблицы, в которой находится текущее значение аргумента х. После нажатия кнопки ОК в ячейку D25 записывается формула
=Fsin($E$22;$H$22;A25),
обеспечивающая вычисление значения функции F(a).
Для вычисления значений функции в точках b и Хср достаточно протянуть формулу, записанную в ячейку D25, по ячейкам Е25 и F25.
В ячейку G25 запишем формулу для определения текущей длины интервала неопределённости
=ABS(B25-A25)
В ячейку H25 запишем формулу, проверки условия (6):
=ЕСЛИ(G25<$F$23;"корень="&ТЕКСТ($C25;"0,000000");"----")
В ячейки А26 и В26 запишем формулы, обеспечивающие на каждом шаге метода дихотомии уменьшение длины интервала неопределённости в два раза. В А26 записывается формула
=ЕСЛИ(D25*F25<0;A25;C25),
а в ячейку В26 формула
=ЕСЛИ(D25*F25<0;C25;B25).
Для записи формул во все остальные ячейки 26-й строки таблицы выделяем ячейки 25-й строки таблицы от ячейки С25 до ячейки Н25 и протягиваем формулы этой строки на строку 26.
Для завершения вычислительного процесса выделяем ячейки 26-й строки от А26 до Н26 и протягиваем вниз по строкам до достижения решения.
На рис. 9 показан фрагмент таблицы и некоторые формулы, записываемые в её ячейки.
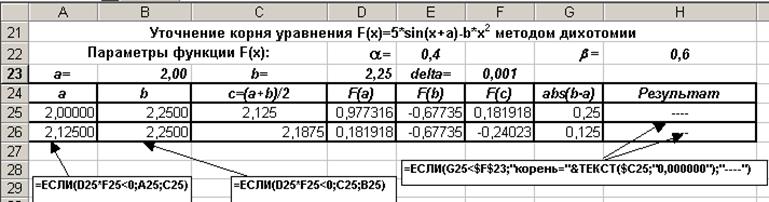 |
Рис. 9.
На рис. 10 показана полная таблица решения уравнения методом дихотомии.
В строке 34 этой таблицы приведены результаты решения, полученные
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.