










Содержание
Введение
Задание
1. Составление линеаризованной модели объекта управления
2. Анализ устойчивости, наблюдаемости, управляемости
2.1 Устойчивость системы
2.2 Управляемость системы
2.3 Наблюдаемость системы
3. Составление разностной модели
3.1. Разностная модель объекта управления
3.2 Разностная модель Пи-регулятора
4. Анализ наблюдаемости, управляемости
4.1 Управляемость системы
4.2 Наблюдаемость системы
5. Замкнутая САУ
6. Моделирование переходного процесса на ЭВМ
Листинг1
Листинг2
Листинг 3
7. Заключение
Тема курсовой работы. Моделирование и анализ цифровой системы управления.
Задание. Объектом управления (ОУ) является процесс изменения уровня в 2-х последовательно соединенных емкостях (рис. 1).
|
|
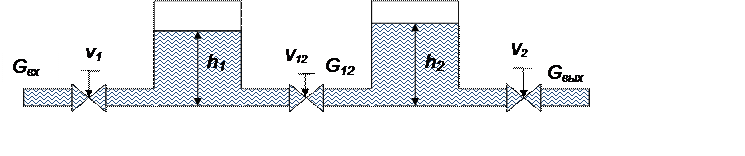
Рис. 1. Объект управления
где: Gвх, Gвых, G12 – расход жидкости на входе, между емкостями и на выходе из
системы:
![]() ;
;
![]() ;
;
![]() ;
;
Fj – площадь поперечного сечения j-ой емкости;
hj – уровень жидкости в емкости j;
vj – положение j-го клапана;
α1, α12, α2 – параметры;
H1, H2 – напор жидкости на выходе и входе.
Изменение уровней в емкостях описывают нелинейные уравнения состояния анализируемой системы (уравнения материального баланса):
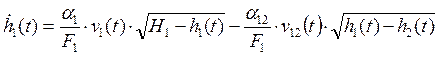 (1)
(1)
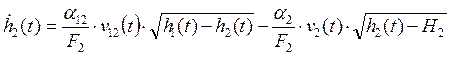 (2)
(2)
Начальные значения уровней в емкостях определяют по уравнениям:
![]() (3)
(3)
![]() (4)
(4)
Уровнемер установлен в емкости, номер j которой указан в таблице вариантов задания. Выходной сигнал уровнемера связан с уровнем уравнением наблюдения:
![]() , (5)
, (5)
где ![]() -
уровень в емкости 2, который определяют моделированием на ЭВМ.
-
уровень в емкости 2, который определяют моделированием на ЭВМ.
Требуемый закон изменения выходной переменной y(t) задан формулой:
. 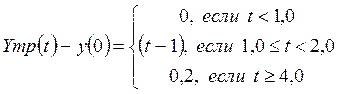 (6)
(6)
При выполнении курсовой работы необходимо:
1. Составить линеаризованную математическую модель ОУ и ПИ-регулятора в пространстве состояний (в виде системы алгебраических и дифференциальных уравнений первого порядка).
2. Выполнить анализ управляемости, наблюдаемости и устойчивости объекта управления.
3. Составить
разностную модель объекта управления (квантование времени выполнить с
постоянным шагом ![]() с.).
с.).
4. Разработать функциональную схему адаптивной системы управления с обучаемой моделью объекта управления.
5. Составить алгоритм формирования управляющего
воздействия, обращающего в минимум критерий обобщенной работы. Параметр
регуляризации выбрать из диапазона: ![]() .
.
6. Моделированием на ЭВМ выполнить анализ качества управления объектом с возмущающим воздействием
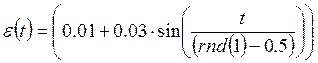 .
.
|
№ варианта |
13 |
|
F1 |
2 |
|
F2 |
1 |
|
H1 |
4 |
|
H2 |
0 |
|
α1 |
1 |
|
α2 |
2 |
|
α12 |
1 |
|
YN |
1,0 |
|
v1(0) |
0,2 |
|
v12(t) |
0,7 |
|
v2(0) |
0,2 |
|
Управляющее воздействие |
v2(t) |
|
Измеряют уровень |
h2(t) |
Введение
В настоящее время широко распространены цифровые системы управления или т.н. адаптивные, которые с изменением возмущающих воздействий автоматически подстраивают коэффициенты регуляторов. Это особенно важно, когда характер возмущений носит спонтанный характер и зачастую эти возмущения вообще не поддаются математическому описанию. Следовательно, коэффициенты в таких системах не являются постоянными, а изменяются.
Адаптивные системы управления несут в себе сложные математические и логические алгоритмы модели объектов. При проектировании таких систем широко применяется моделирование процессов на ЭВМ.
Цель данной работы – получение необходимого управляющего воздействия, которое изменяло бы уровень в заданной емкости по необходимому закону.
1. Составление линеаризованной модели объекта
Запишем уравнения изменения уровня жидкости в емкости 1:
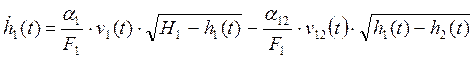
Разложив это
дифференциальное уравнение в ряд Тейлора (принимая ![]() и
и ![]() как постоянные величины)
в дискретные моменты времени и учитывая, что x(t)=h1(t)-h1(tk),
получим:
как постоянные величины)
в дискретные моменты времени и учитывая, что x(t)=h1(t)-h1(tk),
получим:
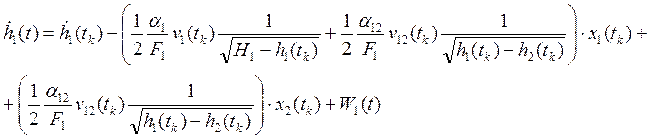
Аналогично: 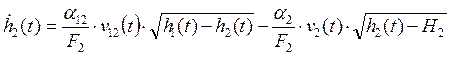 ;
;
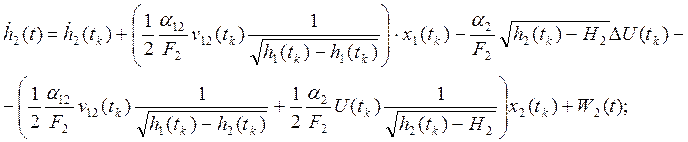
Тогда: 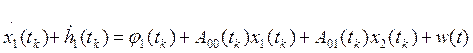 ;
(1*.1)
;
(1*.1)
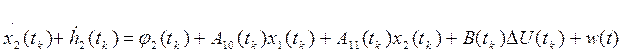 ;
(1*.2)
;
(1*.2)
где 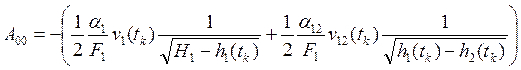
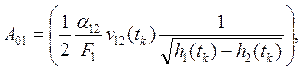
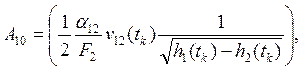
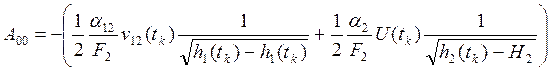
Уравнение наблюдения имеет вид:
![]() где
С – матрица-строка: С=[0;1] (уровнемер установлен в емкости 2)
где
С – матрица-строка: С=[0;1] (уровнемер установлен в емкости 2)
2. Анализ устойчивости, управляемости, наблюдаемости (линеаризованной модели)
2.1. Устойчивая система – система, которая после возмущающего воздействия возвращается в состояние равновесия.
Данную систему можно заведомо считать устойчивой ввиду ее физической природы – в сообщающихся сосудах после некоторого промежутка времени от момента приложения возмущения уровень жидкости становится одинаковым и постоянным в обеих емкостях.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.