Проверка гипотез в задачах корреляционного и регрессионного анализа данных (Практическое занятие № 7)

ВПИ (филиал) ВолгГТУ

Кафедра ВАЭиВТ

Профессор Гольцов А. С.

ПРОВЕРКА ГИПОТЕЗ В ЗАДАЧАХ

КОРРЕЛЯЦИОННОГО И РЕГРЕССИОННОГО АНАЛИЗА ДАННЫХ

Практическое занятие № 7 по дисциплине "Теория систем"

Волжский 2009

1. Методические указания к решению задач

Вероятностно-статистические методы применяют в задачах принятия решений практически во всех случаях, так как обычно возникают такие ситуации, когда между переменными, описывающими систему (явление, процесс), существует так называемая корреляционная зависимость.

          Первоочередная задача корреляционного анализа данных: определение типа зависимости выходной переменной Y от входной переменной X. Если имеем корреляционнуюзависимость, то для определения  функции регрессии необходимо применять методы регрессионного анализа.

Регрессионный анализ в задачах принятия решений выполняют для определения уравнений корреляционной зависимости междуусловным математическим ожиданием =M{Y/X=x_i} случайной выходной переменной Y и случайными входными величинами X иV, принимающими значенияX = { x₁, x₂, …, x_n } и V={ v₁, v₂, …, v_n }.

Количественную меру корреляционной зависимости между случайными величинами Y и X дает функция регрессии:

   ,  i = 1, 2, … , n.                                                               (1)

При решении задач регрессионного анализа необходимо установить определить функцию регрессии  по экспериментальным данным.

Обычно генеральная совокупность неизвестна. Поэтому в корреляционном и регрессионном анализе используют метод выборочных оценок, что существенным образом влияет на достоверность полученных результатов. Достоверность результатов корреляционного и регрессионного анализа устанавливают с помощью проверки статистических гипотез.

Проверка достоверности результатов корреляционного анализа.При выполнении многомерного корреляционного анализа для оценки тесноты корреляционной связи между результирующей переменной и влияющими факторами применяют:

- выборочную оценку коэффициента множественной детерминации D;

- выборочные оценки коэффициентов парной корреляции (либо коэффициентов частной корреляции) r_i,jмежду признаками i и j.

Значимость выборочной оценки коэффициента множественной детерминации определяют проверкой гипотез:

H₀:  D=0;

H₁: D>0

с критерием, наблюдаемое значение которого вычисляют по формуле

,

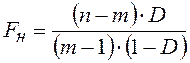где  - объем выборки;  - число влияющих факторов.

Показатель эффективности этого критерия имеет распределение Фишера. Поэтому критическое значение этого показателя  определяют при уровне значимости  по таблицам F-распределения со степенями свободы  и  по уравнению:

.

В скалярном случае (при одном влияющем факторе) значимость коэффициента детерминации определяют по критерию

,

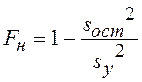где  - выборочная оценка остаточной дисперсии;  - выборочная оценка остаточной дисперсии результирующей переменной.

Показатель эффективности этого критерия имеет распределение Фишера. Поэтому критическое значение этого показателя  определяют при уровне значимости  по таблицам F-распределения со степенями свободы  и  по уравнению:

,

где  - объем выборки;  - число групп вариационного ряда влияющего фактора.

Значимость выборочных оценок коэффициентов парной корреляции (либо коэффициентов частной корреляции) r_i,jмежду признаками i и j определяют проверкой гипотез:

H₀:  r_i,j=0;

H₁: >0

с критерием, наблюдаемое значение которого вычисляют по формуле

,

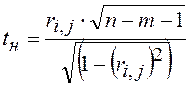где  - объем выборки;  - число влияющих факторов.

Показатель эффективности этого критерия имеет распределение Стьюдента. Поэтому критическое значение этого показателя  определяют при уровне значимости  по таблицам t-распределения со степенью свободы  по уравнению:

.

Проверка достоверности результатов линейного регрессионного анализа.В скалярном случае (при одном влияющем факторе) достоверность результатов линейного регрессионного анализа определяют проверкой значимости коэффициента корреляции . Значимость выборочной оценки коэффициента корреляции определяют проверкой гипотез: