Проверка гипотез в задачах корреляционного и регрессионного анализа данных (Практическое занятие № 7), страница 2

H₀: r=0;

H₁: >0

с критерием, наблюдаемое значение которого вычисляют по формуле

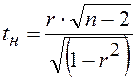где - объем выборки.

Показатель эффективности этого критерия имеет распределение Стьюдента. Поэтому критическое значение этого показателя определяют при уровне значимости по таблицам t-распределения со степенью свободы по уравнению:

В многомерных задачах достоверность линейного регрессионного анализа определяют путем проверки следующих гипотез о значимости уравнения линии регрессии

H₀: уравнение линии регрессии незначимо;

H₁: уравнение линии регрессии значимо

с критерием, наблюдаемое значение которого вычисляют по формуле

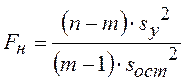где - объем выборки; - число параметров уравнения линии регрессии.

Показатель эффективности этого критерия имеет распределение Фишера. Поэтому критическое значение этого показателя определяют при уровне значимости по таблицам F-распределения со степенями свободы и по уравнению:

2. Задание на самостоятельное решение задач

Задача 1. В журнале Biometrika № 8 на стр. 94 приведены результаты обследования школьников 1725, выполненные Gilby W. H. В таблице 1 приведено полученное распределение этих школьников по значениям двух анализируемых признаков: по качеству одежды Y и по их умственным способностям X. Были определены 4 градации по первому признаку (Y): 1 – "очень хорошо"; 2 – " хорошо"; 3 – "удовлетворительно"; 4 – "плохо". По второму признаку (X) были введены 6 градаций: 1 – "плохие способности"; 2 – " способности ниже средних"; 3 – "средние способности"; 4 – " способности выше средних"; 5 – "высокие способности"; 3 – "превосходные способности".

Табл. 1

	Y		X												Ny
			x₁=1		x₂=2		x₃=3		x₄=4		x₅=5		x₆=6
y₁=1		33		48		113		200		194		39		627
y₂=2		41		100		202		264		138		15		760
y₃=3		39		58		70		61		33		4		265
y₄=4		17		13		22		10		10		1		73
Nx		130		219		407		535		375		59		n=1725

Требуется проверить значимость линейной корреляционной зависимости манеры одеваться от способностей (значимость коэффициента детерминации и коэффициента корреляции).

Задача 2. Необходимо выполнить анализ экономической информации на примере деятельности предприятий одного из регионов страны (данные условные) с помощью регрессионного анализа результатов деятельности предприятий по данным, представленных в таблице 2.

Таблица 2. Данные по годовым отчетам предприятий.

№ предприятия	Себестоимость продукции (млн. руб.)	Объем валовой продукции (млн. руб.)	Производительность (тыс. руб. на чел.)
1	2,1	3	18
2	2,8	4	15
3	3,2	5	14
4	4.5	5	13
5	4,8	5	13
6	4,9	5	15
7	5,5	6	16
8	6,5	7	12
9	12,1	15	13
10	15,0	20	12

По результатам анализа сделать обоснованное заключение о выявленной взаимосвязи показателей эффективности производства.

Результаты анализа занесите в рабочую тетрадь.

Профессор А. Гольцов

1 2

Скачать файл