Моделирование и анализ цифровой системы управления, страница 2

2.2 Управляемой называют систему, которую можно привести из любого начального состояния в требуемое с помощью выбранного набора управляющих воздействий за ограниченный промежуток времени.

Для анализа управляемости используем критерий управляемости Калмана.

Введена матрица Q:                            , ранг которой равен                  ,

при этом n (– число переменных состояния) = 2. Согласно вышеприведенному критерию система управляема, если ранг матрицы управляемости (Q)равен числу переменных состояния (n). Следовательно, система управляема.

2.3  Наблюдаемой называют такую систему, в которой по измеренным выходным сигналам можно определить все переменные состояния в любой момент времени.

Для анализа наблюдаемости используем критерий наблюдаемости Калмана.

Введена матрица   N = [C^T,(CA)^T], ранг которой равен                     . Для того,

Чтобы система была наблюдаемой достаточно, чтобы ранг матрицы наблюдаемости (N) был равен числу переменных состояния (n). Это условие выполнено.

3.1 Разностная модель объекта управления

Исходные данные – уравнения (1*.1) и (1*.2)

. Проводим квантование по времени и решаем эти уравнения по методу Эйлера, при этом заменяя  . Шаг квантования выбираем т.о., чтобы выполнялась теорема Котельникова  (в данном случае принят шаг квантования 0,01 с и теорема Котельникова заведомо выполняется).

Тогда имеем: 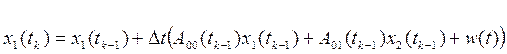   (3*1.1)

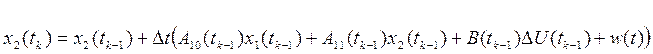  (3*1.2)

и

Т.е.: 

         

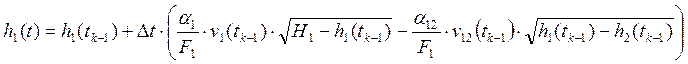
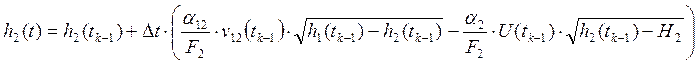
3.2 Разностная модель Пи-регулятора

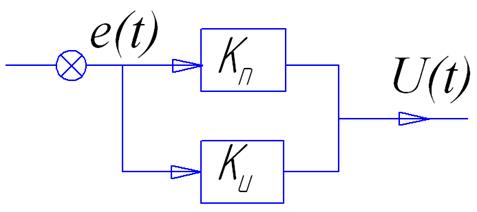
Математическая модель регулятора имеет вид:

Выразим второе слагаемое рекуррентным методом:   e(t)=y_тр(t)-y(t)=y(t)-C·x(t);    (3*2.1)

  S(t_k) ≈ S(t_k-1)+e(t_k-1)·k_и·Δt;                                                  (3*2.2)

  Тогда:              (3*2.3)

   4. Анализ устойчивости, управляемости, наблюдаемости (разностной     модели)

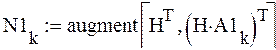
4.1. Полученная система с разностными моделями объекта управления и регулятора также будет управляема на основе выполнения критерия управляемости Калмана:                                           , при этом ранг в k-й момент времени равен 2, n=2.  

4.2 Критерий наблюдаемости также выполняется:                                                     

Ранг этой матрицы также равен 2 k-й момент времени равен 2, n=2.  

Значит полученная система с разностными моделями объекта управления и регулятора управляема и наблюдаема.

5. Замкнутая САУ

Схема имеет вид:

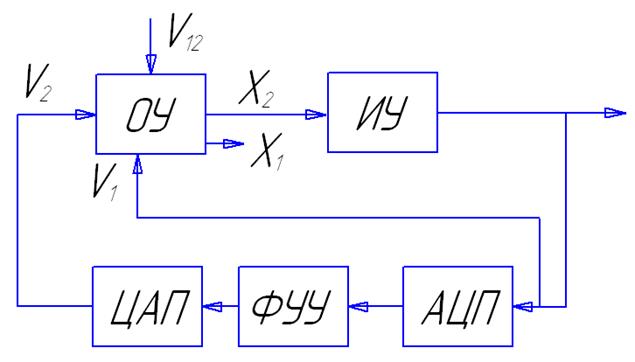
Представим уравнения (3*1.1), (3*1.2), (3*2.1)- (3*2.3) в матричном виде, для этого введем матрицы:

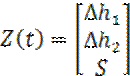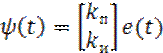,  ,  H=[C;0],  ,   

e(t_k)=y_тр(t_k)-HZ(t_k),     

Управляющее воздействие V2(t) и оптимальные коэффициенты регулятора (переменные) определяются путем минимизации ФОР.

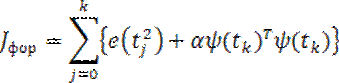
Для нахождения минимума ФОР используем принцип максимума.

Для линеаризованной модели:  ;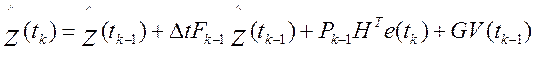

,

где 𝛼 – параметр регуляризации (количественное выражение предпочтения затратам или погрешности).

Тогда

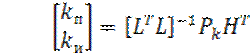
6. Моделирование переходного процесса.

Использован пакет MathCAD со стандартным набором функций.

При моделировании в невязку сигналов добавляется шум: yтр-(h2+).

Листинг1 – Линеаризация.

            

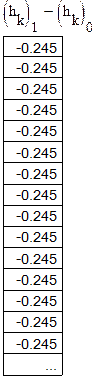
Листинг 2 – Анализ и составление разностной модели

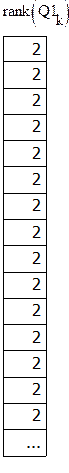
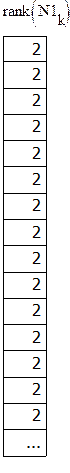
Листинг 3 – Замкнутая САУ, поиск настроечных коэффициентов

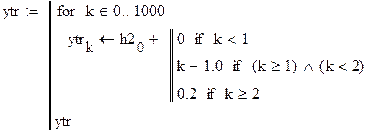
Заключение

    Для нахождения необходимого управляющего воздействия был применен алгоритм минимизации функционала обобщенной работы, для чего исходная модель заменена линеаризованной.  Абсолютная погрешность  - 0,245 единиц, относительная -

   Затем была составлена разностная модель объекта управления и регулятора с целью нахождения их текущего значения по предыдущему с заданным шагом квантования.

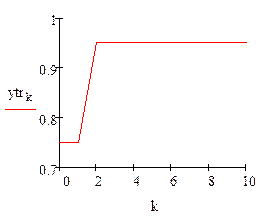
   В замкнутой системе получены коэффициенты регулятора и оптимальный параметр регуляризации (𝛼=0,009) при котором наблюдается небольшое перерегулирование. Статическая погрешность равна 0 ((y_тр)₁₀₀₀-h2₁₀₀₀).