Разработка алгоритма декомпозиции адаптивной системы автоматического управления технологическими процессами

А. С. Гольцов

РАЗРАБОТКА АЛГОРИТМА ДЕКОМПОЗИЦИИ АДАПТИВНОЙ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ТЕХНОЛОГИЧЕСКИМИ ПРОЦЕССАМИ

В традиционных системах оптимального (и адаптивного) управления для формирования управляющих воздействий в контур обратной связи системы управления включают наблюдатель переменных состояния - вычислительный блок, с помощью которого вычисляют оценки всех переменных состояния объекта управления. Полученные оценки переменных состояния используют для формирования управляющих воздействий. Однако если некоторые переменные состояния непосредственно измеряют, то нет необходимости вычисления их оценок. Поэтому выполняют декомпозицию модели состояния объекта управления: в системе управления применяют наблюдатели состояния пониженного порядка, которые вычисляют оценки только переменных состояния, не доступных для непосредственного измерения. Это позволяет существенно уменьшить объем вычислений при реализации алгоритмов управления многомерными объектами [1].

В то же время качество управления технологическими процессами обычно определяют по отклонению (невязкам) части переменных состояния объекта управления (управляемых переменных) от их требуемых значений, формируемых задатчиком системы управления. Например, в объекте -го порядка с одним управляющим воздействием и одной управляемой переменной в алгоритмах ПИ-регулирования используют только невязку между требуемыми и реализованными значениями управляемой переменной. При этом реализованные значения управляемой переменной обычно получают непосредственными измерениями. В таких системах управления имеется возможность дополнительно уменьшить размерность системы дифференциальных уравнений, используемых для формирования управляющих воздействий.

1.  Постановка задачи

Модель объекта управления в пространстве состояний. Пусть объект управления представляет собой систему, образованную из  звеньев (элементов) с одним управляющим воздействием  и одной управляемой переменной . Динамику объекта управления описывают уравнения состояния в наблюдаемой канонической форме

                                                 (1.1)

с начальными условиями

,                                                                                                            (1.2)

где:

 - вектор переменных состояния, который содержит управляемую переменную , но из него исключены выходные сигналы звеньев, доступные измерениям;

 - параметр, имеющий размерность времени (например, постоянная времени одного из элементов объекта управления);

  - вектор, образованный входными и выходными сигналами звеньев объекта управления, доступными непосредственным измерениям;

             - вектор неконтролируемых (возмущающих) входных воздействий.

Матрицы  и  

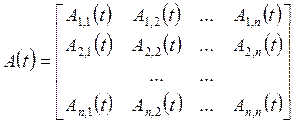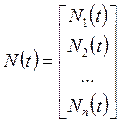;   ;   ,               (1.3)

содержат элементы, часть которых может равняться нулю, но   не равен нулю.

Управляемая переменная (переменная состояния  с номером ) доступна измерениям. Измеренные значения управляемой переменной  связаны с переменными состояния уравнением:

,                                                                                   (1.4)

где  - погрешность измерений.

            Предполагается, что система (1.1) - (1.4) управляема и наблюдаема.

            Модель ПИ-регулятора в пространстве состояний. Задатчик системы управления формирует требуемые значения управляемой переменной в виде заданной функции времени . При этом выходной сигнал объекта управления должен быть связан с требуемым значением управляемой переменной уравнением:

,                                                                              (1.5)

где  - допустимая погрешность управления.

Управляющее воздействие формирует ПИ-регулятор по алгоритму:

;                                                                                  (1.6)

;                                                                                        (1.7)

,                                                                                        (1.8)

где:

,                                                                              (1.9)

 и  - параметры настройки регулятора, подлежащие определению. 

Функционал обобщенной работы системы управления.Параметры настройки регулятора должны обращать в минимум функционал обобщенной работы (ФОР) [2]

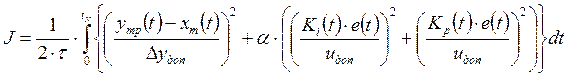,                (1.10)

где  - весовой коэффициент (параметр регуляризации).

2.  Вывод алгоритма настройки параметров ПИ-регулятора

Декомпозиция модели объекта управления на две подсистемы.Из переменных состояния объекта управления сформируем два вектора:

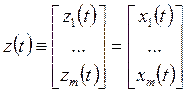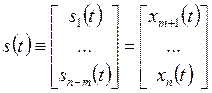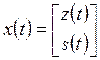;     ;    .                    (2.1)

Тогда систему уравнений (1.1) можно разделить на две подсистемы уравнений:

;                                                 (2.2)

,                                                 (2.3)

где:

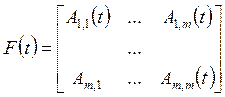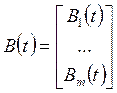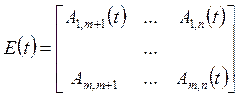;  ;  ;          (2.4)

;  ;   ;

;    .

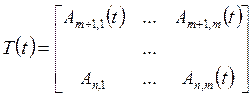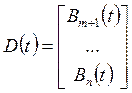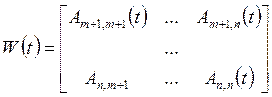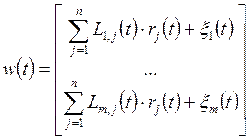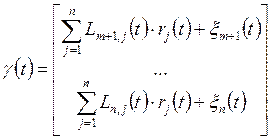При этом уравнение (1.4) после замены переменных можно записать в следующем виде:

,                                                                            (2.5)

где

.