Моделирование системы управления разделением сероуглерода

3 Моделирование системы управления

Технологическим объектом управления выбрана промежуточная ёмкость, где происходит разделение сероуглерода, содержащего воду, на сероуглерод и воду.

Задача автоматического регулирования заключается в достижении заданной чёткости разделения исходной смеси. Содержание сероуглерода и керосина-растворителя в промежуточной ёмкости не должно превышать 0,9% при максимально возможной производительности и экономичности процесса. Поэтому необходимо регулирование уровня в промежуточной ёмкости путём изменения расхода сероуглерода на склад.

3.1 Математическое описание объекта

Для определения передаточной функции объекта управления необходимо получить экспериментальную кривую разгона. Для этого провели эксперимент. При положении задвижки, регулирующей уровень в емкости, соответствующем 5% от полного прикрыли задвижку на 70%, то есть на 65% от полного хода. Примем, что задвижка открывается достаточно быстро (по сравнению с ожидаемой длительностью переходного процесса), то есть такое воздействие на исследуемый объект можно считать ступенчатым. Для исследования объектов, которые предполагаются линейными «неединичность» ступенчатого воздействия никакой роли не играет и легко учитывается соответствующим изменением рассчитанного коэффициента передачи.

В результате эксперимента получили следующие данные:

Таблица 3.1 Изменение уровня в емкости

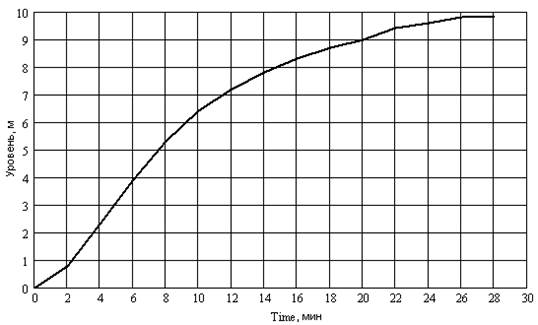
Рисунок 3.1 – График кривой разгона объекта управления

Строим кривую разгона в относительных координатах уровня:

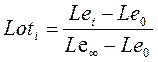, где                                                                           (3.1)

Lot_i – аппроксимирующая функция;

Le_i , Le_∞ , Le₀  – экспериментальные данные.

График зависимости относительного уровня от времени представлен на рисунке 3.2.

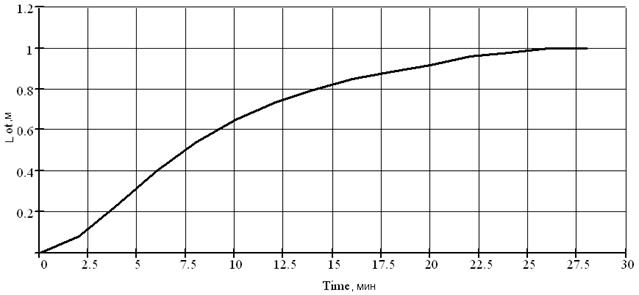
Рисунок 3.2 – График кривой разгона при относительной температуре

Дла построения математической модели использована из анализа рисунка 3.2 сделан вывод что можно использовать звено ІІ порядка.

Предположим, что зависимость уровня в емкости от расхода можно описать передаточной функцией апериодического звена второго порядка. Таким образом, передаточная функция может быть представлена в виде:

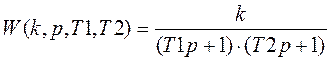                             (3.2)

где  k, Т₁, Т₂ – подлежат определению по эксперементальной кривой разгона.

Определим переходную характеристику для данной передаточной функции.

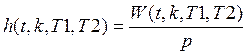                                                                         (3.3)

Найдем передаточную функцию в программном средстве MathCAD, используя функцию minimize, способом минимизации суммы квадратов отклонений значений экспериментальных данных и аппроксимирующей функции:

                                                       ,                               (3.4)

где Lot_i – аппроксимирующая функция;

Le_i – экспериментальные данные.

Таким образом, получим что:

                                     

при:

k = 1;

T1 = 3,07;

T2 = 6,069.

Построим два графика зависимости (рисунок 3.3):

1.  кривая разгона объекта управления (обз. точками),

2.  теоретическую характеристику (обз. сплошной линией):

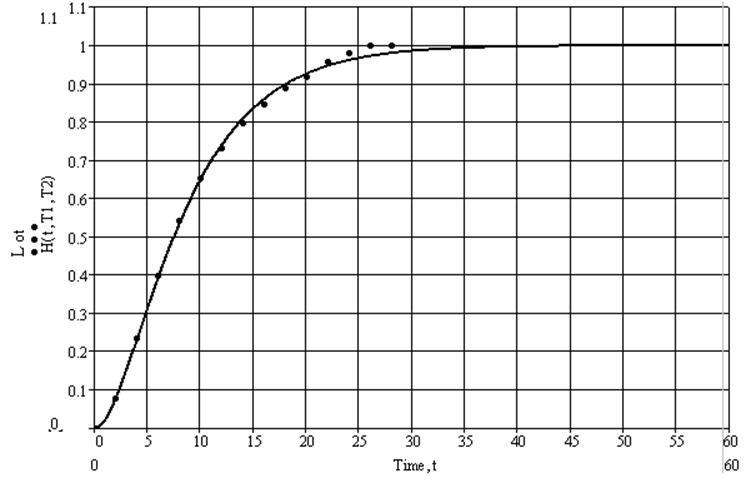
Рисунок 3.3 – Кривая разгона и теоретическая характеристика, рассчитанная по методу наименьших квадратов

3.2 Анализ управляемости и наблюдаемости

Передаточная функция объекта имеет вид:

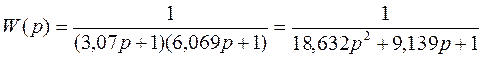
Представим уравнение в пространстве состояний. Умножим знаменатель на Y(p) получим:

                                                           (3.5)    

Представим замену в виде системы уравнений:

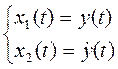                            ,                                                          (3.6)

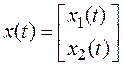                                                        (3.7)

.                                                (3.8)

где ε – статическая погрешность.

В расчете статической погрешностью можно пренебречь и условно считать равной нулю.

Напишем модель в пространстве состояний:

                                     (3.9)

где  – неконтролируемое возмущающее воздействие;

А, В, G – матрицы для анализа основных свойств системы.

В расчете неконтролируемым возмущающим воздействием можно пренебречь и условно считать равным нулю.

Запишем уравнение наблюдаемости:

.                                              (3.10)

где С – матрица для анализа основных свойств системы.

Сравнивая уравнения (3.9) и (3.10) можно определить матрицу С.

.                                                    (3.11)

Из уравнения (3.10) получим:

.        (3.12)

Продифференцируем второе уравнение из системы уравнений (3.6), получим:

.                                                   (3.13)

Подставив в уравнение (3.5), получаем:

.                         (3.14)

Разделим обе части уравнения (3.14) на , получаем:

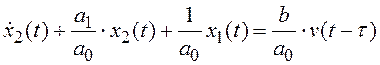.                           (3.15)

Перенеся все известные величины в правую часть, получаем:

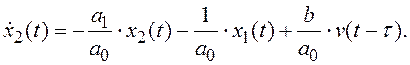                       (3.16)

          

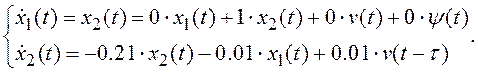               (3.17)

Решая систему уравнений (3.17), получаем:

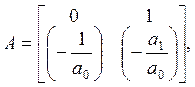                                                (3.18)

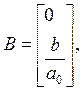                                                      (3.19)

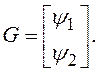                                                     (3.20)

где значения матриц  А, В, G –коэффициенты при  соответственно.

                                     

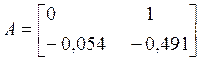
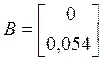
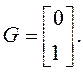
3.2.1  Анализ управляемости