Моделирование системы управления разделением сероуглерода, страница 2

По критерию Калмана в рассматриваемой системе ранг матрицы Q должен быть больше 0 для управляемой системы. Так как в данном проекте система уравнений состоит из двух уравнений, то n принят равным 2. Для анализа управляемости системы составлена матрица управляемости Q.

.                                        (3.21)

.                                      (3.22)

 .

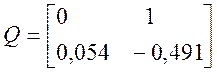Ранг матрицы равен rank(Q)=2 , так как матрица имеет две строки и два столбца.

Так как, количество переменных состояния n = rank(Q), следовательно, система управляема.

3.2.2  Анализ наблюдаемости

В рассматриваемой системе ранг матрицы N должен быть больше 0 для наблюдаемой системы. Для анализа наблюдаемости системы составлена матрица наблюдаемости N. Наблюдаема система будет тогда, когда rank(N)=n.

                                                                                                                                                          (3.23)

После вычислений в программном средстве Mathcad она имеет вид:

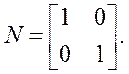
Система наблюдаема, так как rank(N)=n=2.

3.3 Анализ устойчивости объекта

Так как модель обьекта управляема и наблюдаема, следовательно обьект является устойчив.

3.4 Определение настроек ПИ-регулятора

Выходной сигнал ПИ-регулятора пропорционален взвешенной сумме входного сигнала и интеграла от него.

ПИ – регулятор простыми средствами одновременно улучшает качество установившегося режима работы исходной статической САР, и сохраняет качество переходного, чем и обусловлено широкое распространение таких регуляторов.

Структурная схема исследуемой системы с ПИ – регулятором представлена на рисунке 3.5.

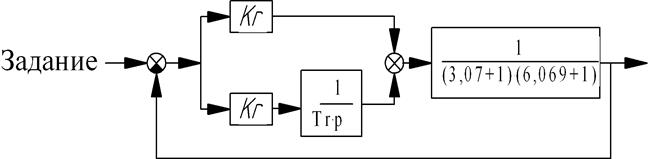
Рисунок 3.4 - Структурная схема системы с ПИ – регулятором

где Kr – пропорциональный коэффициент регулирования;

Tr – постоянная времени регулятора.

Рассчитаем параметры регулятора методом расширенной АФЧХ.

Основу метода составляет обобщенный критерий Найквиста:

Замкнутая система является устойчивой, если АФЧХ разомкнутой системы не охватывает точку −(-1,0) комплексной плоскости.

Построим АФЧХ полученной передаточной функции разомкнутой системы (рисунок 3.5):

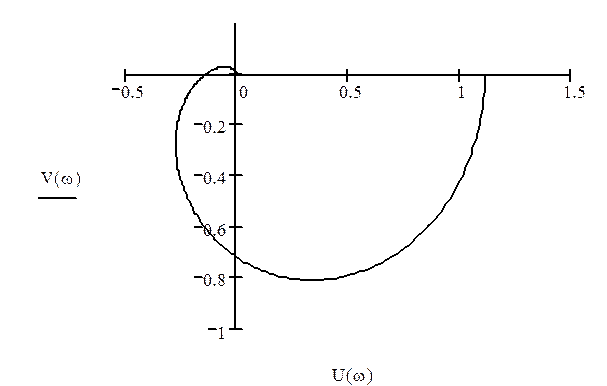
Рисунок 3.5 – АФЧХ передаточной функции

V(ω) = Im(W(ω));

U(ω) = Re(W(ω)).

Так как АФЧХ передаточной функции не охватывает точку (-1,0) процесс

является устойчивым.  

 Разомкнутая линейная система, имеющая корневой показатель колебательности не хуже m, сохранит его и после замыкания отрицательной обратной связью, если расширенная АФЧХ разомкнутой системы:

                                                           (3.24)

не охватывает на комплексной плоскости точку (-1;j×0),

где m – коэффициент запаса устойчивости (m=0,9);

W_раз(ω) - передаточная функция разомкнутой системы:

         W_раз(ω) = Wo(ω)∙W_рег(ω),                                                          (3.25)

где Wo(ω) – передаточная функция объекта управления;

W_рег(ω) – передаточная функция регулятора.

В предельном случае расширенная АФЧХ должна проходить через точку  (-1;j×0).

В теории автоматического управления доказывается, что в замкнутых

системах автоматического регулирования с ПИ-регулятором минимум интеграла от квадрата ошибки:

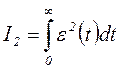                                                                                        (3.26)

достигается при

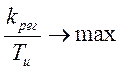                              ,                                                         (3.27)

где k_рег – коэффициент передачи ПИ-регулятора;

Т_и – постоянная времени интегрирования.

Расчет параметров ПИ-регулятора будем производить в программном средстве MathCAD.

Передаточная функция ПИ-регулятора как функция пока еще неизвестных параметров kr и Tr – коэффициента передачи и постоянной времени интегрирования регулятора:

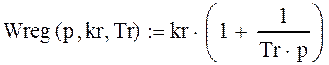               .                                     (3.28)

Составим передаточную функцию разомкнутой системы:

         .

Запишем в общем виде расширенную передаточную функцию разомкнутой системы:

,

ее действительную и мнимую части:

                    

                     .

Запишем функцию, максимум которой будет соответствовать оптимальным параметрам настройки регулятора:

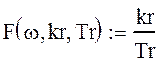                           ,                                                     (3.29)

В программном средстве MathCAD, используя функцию maximaize, находим максимум функции F(ω,kr,Tr) со следующими ограничениями:

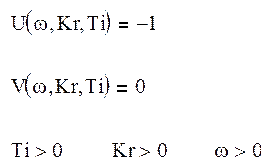
Функция F(ω,kr,Tr) будет будет максимальна если:

Kr = 1,117;

Ti = 6,138.

Построим переходную характеристику замкнутой системы при изменении задания на регулирование.

Передаточная функция замкнутой системы:

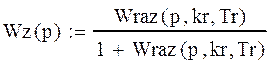               .                                               (3.30)

Переходная функция определена стандартом пакетом программ MathCAD с использованными функциями:

             .

Результаты вычислений представлены на рисунке 3.6

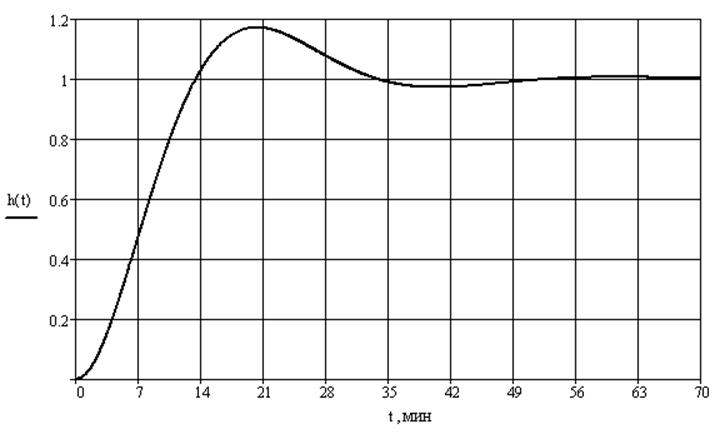
Рисунок 3.6 – Переходная характеристика замкнутой системы при определении оптимальных параметров настройки регулятора методом расширенной АФЧХ

Анализ качества системы управления:

Проведем проверку системы с ПИ-регулятором на качество:

Анализ выполняется по прямым.

Статические критерии качества:

Перерегулирование 17%.

Динамические критерии качества:

Время регулирования Т_рег = 30,94 мин;

Время нарастания Т_{наростания} = 13.44;

Скорость переходного процесса определяем по переходному процессу объекта регулирования:

α = 97.

Вывод: по сравнению с действующей системой были сформированы и решены основные задачи оптимизации системы управления, такие как составление разностоной математической модели обьекта управления. Был произведен анализ наблюдаемости и управляемости обьекта управления, анализ качества управления обьектаом.