Примечание.
Декомпозицию модели объекта управления следует выполнить так, чтобы при
обеспечении минимальной размерности вектора переменных ![]() система
(2.2), (2.5) была управляемой по входу
система
(2.2), (2.5) была управляемой по входу ![]() и наблюдаемой
по управляемой переменной
и наблюдаемой
по управляемой переменной ![]() .
.
Если указанные условия выполняются, то для определения параметров ПИ-регулятора (1.6) - (1.8), обеспечивающих минимум ФОР (1.10), можно использовать только подсистему (2.2).
Алгоритм
формирования оптимальных траекторий для переменных состояния системы управления.Уравнения (2.2), (1.6) и (1.7) можно объединить в одно матичное
дифференциальное уравнение для вектора переменных состояния системы управления
(содержащего выходной сигнал ![]() интегрирующего блока регулятора
и части переменных состояния объекта управления
интегрирующего блока регулятора
и части переменных состояния объекта управления ![]() ):
):
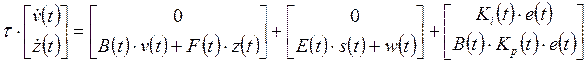 . (2.6)
. (2.6)
Минимизация ФОР (1.10) с ограничениями (2.2) с помощью принципа максимума приводит к следующей системе дифференциальных уравнений, описывающей оптимальные траектории изменения во времени всех переменных состояния объекта управления и выходного сигнала интегрирующего блока ПИ-регулятора:
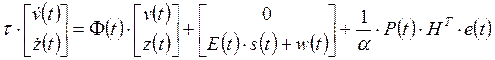 ;
; ![]() ;
; ![]() ; (2.7)
; (2.7)
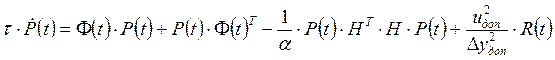 ;
;
![]() , (2.8)
, (2.8)
где блочные матрицы ![]() ,
, ![]() и
и ![]() составлены следующим образом:
составлены следующим образом:
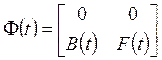 ;
; ![]() ;
; 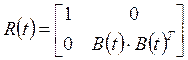 ; (2.9)
; (2.9)
![]() -
квадратная матрица размерностью
-
квадратная матрица размерностью ![]() .
.
Алгоритм настройки параметров ПИ-регулятора.Из равенства правых и левых частей уравнений (2,2) и (2.7) следует уравнение
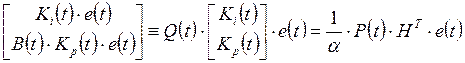 , (2.10)
, (2.10)
из которого получим формулу для вычисления параметров ПИ-регулятора:
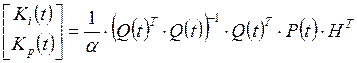 , (2.11)
, (2.11)
где блочная матрица ![]() , которая имеет размерность 2´(1+m), составлена следующим образом:
, которая имеет размерность 2´(1+m), составлена следующим образом:
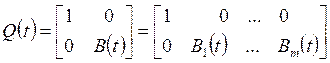 .
(2.12)
.
(2.12)
Выводы. Таким образом, для линейного объекта управления (2.1) минимизацией функционала обобщенной работы (1.10) получен алгоритм настройки параметров ПИ-регулятора, из которого следует, что:
1. Параметры ПИ-регулятора, обращающие в минимум ФОР (1.10), изменяются в процессе управления;
2. При вычислении параметров ПИ-регулятора числовые значения переменных состояния объекта управления не используются;
3. Алгоритм настройки параметров ПИ-регулятора включает в себя:
3.1. Декомпозицию исходной модели объекта управления (2.1) на две подсистемы (2.2) и (2.3);
3.2. Составление
для подсистемы (2.2) дифференциального уравнения Риккати (2.8). Параметр
регуляризации ![]() следует выбирать по условию
обеспечения асимптотической устойчивости численного решения этого уравнения;
следует выбирать по условию
обеспечения асимптотической устойчивости численного решения этого уравнения;
3.3. Вычисление
текущих значений матрицы вспомогательных переменных ![]() ,
имеющей размерность (m+1)´(m+1),
численным интегрированием уравнения (2.8);
,
имеющей размерность (m+1)´(m+1),
численным интегрированием уравнения (2.8);
3.4. Вычисление текущих значений параметров ПИ-регулятора по формуле (2.11);
Пример. Пусть
управляемая переменная ![]() является выходным сигналом
элемента объекта управления, на вход которого поступает управляющее воздействие
является выходным сигналом
элемента объекта управления, на вход которого поступает управляющее воздействие
![]() , т.е. совпадает с переменной состояния
объекта управления
, т.е. совпадает с переменной состояния
объекта управления ![]() и
и ![]() :
:
![]() .
(1.4a)
.
(1.4a)
Из уравнений динамики (1.1) и (1.7) с учетом выражений (1.6) и (1.8) сформируем систему уравнений:
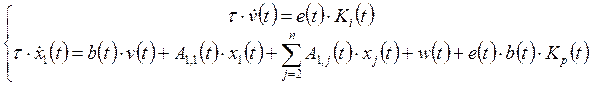 ,
(2.13)
,
(2.13)
где
![]() ;
; 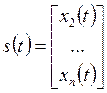 ;
; 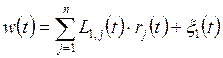 . (2.14)
. (2.14)
Сформируем векторы вспомогательных переменных
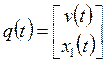 ;
; 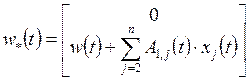 ;
; 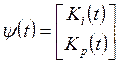
и матрицы
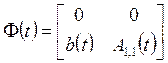 ;
; 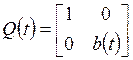 ;
; ![]() .
.
Тогда уравнения (2.1) и формулу (1.10) для ФОР можно записать в следующем эквивалентном виде:
![]() ;
;
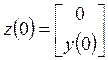 ; (2.15)
; (2.15)
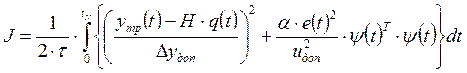 .
(2.16)
.
(2.16)
Следовательно,
параметры ПИ-регулятора можно определить минимизацией ФОР (2.16) по переменным ![]() и
и ![]() с
учетом ограничений, создаваемых дифференциальным уравнением (2.15). В
результате решения этой задачи условной минимизации с помощью принципа
максимума были получены следующие уравнения для оптимальных значений вектора
переменных
с
учетом ограничений, создаваемых дифференциальным уравнением (2.15). В
результате решения этой задачи условной минимизации с помощью принципа
максимума были получены следующие уравнения для оптимальных значений вектора
переменных ![]() :
:
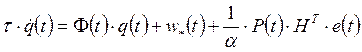 ;
;
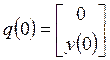 ; (2.17)
; (2.17)
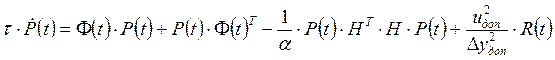 ;
;
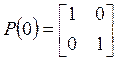 , (2.18)
, (2.18)
где:
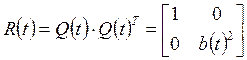 . (2.19)
. (2.19)
Из равенства правых и левых частей уравнений (2.15) и (2.17) получим формулу для вычисления параметров настройки ПИ-регулятора:
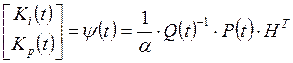 ,
,
или (учитывая формулы (2.14) для
формирования матриц ![]() и
и ![]() ):
):
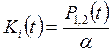 ;
;
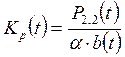 , (2.20)
, (2.20)
где ![]() и
и ![]() -
элементы квадратной матрицы
-
элементы квадратной матрицы ![]() , имеющей размерность (2´2), текущие значения которых вычисляют путем
решения дифференциального уравнения (2.18).
, имеющей размерность (2´2), текущие значения которых вычисляют путем
решения дифференциального уравнения (2.18).
Список использованной литературы
1. Гудвин Г.К., Гребе С.Ф., Сальгадо М.Э. Проектирование систем управления. - М.: ВИНОМ, 2004. - 911 с.
2. Гольцов А. С. Адаптивные системы автоматического управления нелинейными объектами. - Орел: Академия ФАПСИ, 2002. – 156 c.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.