Разработка информационно-измерительной системы контроля полезной мощности печи сопротивления, страница 6

Формы начальных участков зависимостей сопротивлений блока  и  на рис. 2.15  подтверждают правильность предположения о более быстром изменении этих параметров в сравнении с параметрами , , , которые являются характеристиками изоляции печи. Общая проводимость электрической цепи между точками подключения вольтметров (рис. 2.11) близка к результатам “холодных” измерений перед включением трансформатора. Довольно большая разность между значениями  и  на протяжении всей плавки можно интерпретировать как показатель не очень хорошей равномерности загрузки шихты и керна.

Из рис. 2.16 видно, что сопротивления ,  расположены в отрицательной области, то есть печь является активно-ёмкостной нагрузкой. По виду сопротивлений ,, (рис. 2.17) можно сделать вывод о том, что характер сопротивлений может быть как активно-индуктивным (), так и активно-ёмкостным (). Сопротивление  большую часть плавки является чисто активным для рассмотренного примера.

Из графика полученного решения для φ₁ (рис. 2.18) видно, что сдвиг фаз резко изменяется примерно через 8 часов после начала плавки. Можно заметить, что это произошло после того, как закончились нелинейные колебания в динамике роста активной мощности (или тока) печи (рис. 2.13). Возможно, это связано с началом образования кристаллов карбида кремния в печи.

Электрическая проводимость печи может быть найдена по формуле:

Результаты определения проводимости для нескольких плавок в течение одной плавильной кампании показаны на рис. 2.19. Электрическая проводимость печи является инерционным и достаточно медленно изменяющимся параметром, характеризующим состояние печи сопротивления в текущий момент времени. Вследствие образования карбида кремния и других причин [30] проводимость печи непрерывно растёт.

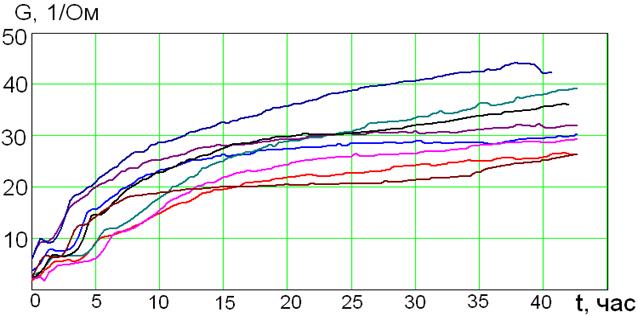
Рисунок 2.19 − Графики изменения проводимости печи сопротивления, рассчитанные для нескольких плавок

Из полученных графиков изменения проводимости видно, что, несмотря на довольно точную загрузку сырьевых компонентов шихты,  динамика роста электрической проводимости шихты для различных печей различна. Это подтверждает предположение о том, что разные печи обладают разным  качеством изоляции. За весь период плавильной кампании проводимость в среднем возрастает в 6-7 раз, что согласуется с данными, приведёнными в литературе [30].

Знание динамики изменения проводимости печи (или ее электрического сопротивления) является важным для технологов цеха. По виду графика роста проводимости можно судить о равномерности образования SiC.

Полезная мощность печи сопротивления может быть найдена по результатам решения системы уравнений (2.8):

Можно также выразить полезную мощность через электрическую проводимость печи:

где U− падение напряжения на печи.

Приведённое выражение может быть использовано в дальнейшем при построении математической модели печи сопротивления в пространстве состояний.

2.2.2 Алгоритм расчёта полезной мощности для ЭВМ

Составлена блок-схема алгоритма определения электрических параметров печи сопротивления:

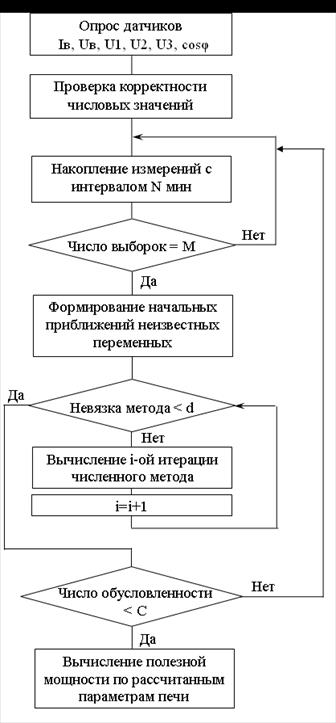
Рис. 2.20 − Алгоритм вычисления полезной мощности печи в реальном времени на ЭВМ

На первом этапе производится опрос датчиков электрических параметров: I_В, U_В, U₁, U₂, U₃, cosφ. Далее значения, считанные с датчиков, проверяются на корректность. Для этого можно использовать алгоритмы проверки на выброс, обрыв, замирание сигнала. Если данные корректны, то они помещаются в накопитель. Новые данные считываются с интервалом N минут. Длина интервала была найдена экспериментально и обеспечивает невырожденность системы (2.8). Когда число выборок составляет M, формируются начальные приближения для неизвестных переменных и запускается цикл выполнения итераций по методу Левенберга-Марквардта [27, 85]. Согласно методу очередная итерация вычисляется по формуле:

где

 − новое приближение к решению;

− вектор приближения, вычисленный на предыдущем шаге;

− параметр метода, ; выбирается по правилам, описанным в [85];

 − единичная матрица;

− вектор функций системы (2.8);

 − матрица Якоби (или Якобиан):

На каждом шаге проверяется значение средней невязки метода. Как только становится ясно, что новые шаги не приводят к уменьшению невязки, цикл останавливается. По найденным значениям вычисляется число обусловленности системы: