Фазы напряжений ![]() ,
, ![]() неизвестны, однако, если принять, что
фаза вектора
неизвестны, однако, если принять, что
фаза вектора ![]() полного
падения напряжения на печи равна нулю, то могут быть записаны выражения (2.4). Угол
φ1 также следует считать неизвестным при решении системы (2.2). Уравнения
(2.4) записаны для случая, когда вольтметр
полного
падения напряжения на печи равна нулю, то могут быть записаны выражения (2.4). Угол
φ1 также следует считать неизвестным при решении системы (2.2). Уравнения
(2.4) записаны для случая, когда вольтметр ![]() подключён к стороне с длинным
участком короткой сети.
подключён к стороне с длинным
участком короткой сети.
Текущий коэффициент трансформации kможно определить из выражения:
|
|
(2.5) |
Возможно определение коэффициента трансформации из паспортных данных трансформатора для текущей ступени, однако вычисление по формуле (2.5) даст более точное значение k.
После исключения из
системы (2.2) контурных токов ![]() ,
, ![]() и
и ![]() система
(2.2) примет следующий вид:
система
(2.2) примет следующий вид:
|
|
(2.6) |
В качестве неизвестных
для этой системы из 3-х уравнений следует рассматривать электрические параметры
модели, зависящие от времени: ![]() ,
,![]() ,
а также параметры, которые меняются относительно медленно в течении одной
плавки:
,
а также параметры, которые меняются относительно медленно в течении одной
плавки: ![]() ,
,![]() ,
,![]() ,φ1.
Сопротивление короткой сети
,φ1.
Сопротивление короткой сети ![]() можно считать
постоянным. Его приближенное значение взято из литературы по исследованию
коротких сетей плавильных установок [26].
можно считать
постоянным. Его приближенное значение взято из литературы по исследованию
коротких сетей плавильных установок [26].
Система уравнений (2.6) является недоопределённой, так как количество неизвестных больше количества уравнений. Система является нелинейной относительно неизвестных переменных, и для её решения необходимо назначать начальные приближения неизвестных переменных и использовать методы решения систем нелинейных уравнений (СНУ) [4,5,27, 33, 79].
Считая ![]() ,
,![]() неизвестными в каждый
момент времени общее количество неизвестных будет равно 12. Условия
определённости системы уравнений можно выполнить, если рассматривать не один
момент времени, а 4 или более различных моментов времени. Также, важно, чтобы
измеряемые электрические величины, входящие в систему, в эти моменты времени имели
различающиеся значения, что должно обеспечить невырожденность системы уравнений
(2.6). Условие невырожденности необходимо для получения правильных решений.
Систему уравнений (2.6), относящуюся к моменту
неизвестными в каждый
момент времени общее количество неизвестных будет равно 12. Условия
определённости системы уравнений можно выполнить, если рассматривать не один
момент времени, а 4 или более различных моментов времени. Также, важно, чтобы
измеряемые электрические величины, входящие в систему, в эти моменты времени имели
различающиеся значения, что должно обеспечить невырожденность системы уравнений
(2.6). Условие невырожденности необходимо для получения правильных решений.
Систему уравнений (2.6), относящуюся к моменту ![]() ,
целесообразно представить в операторной форме, отображающей зависимость от
времени неизвестных сопротивлений и измеряемых величин:
,
целесообразно представить в операторной форме, отображающей зависимость от
времени неизвестных сопротивлений и измеряемых величин:
|
|
(2.7) |
Варьирование моментов
времени измерений позволяет выполнить условия определённости системы (2.7), то
есть число уравнений должно быть равно или больше числа неизвестных. Система
уравнений (2.7) повторяется для каждого момента измерений, образуя новую
систему для групп моментов измерений ![]() . В таком случае
минимальное число уравнений будет равно 12, и соответствующая система будет
иметь вид:
. В таком случае
минимальное число уравнений будет равно 12, и соответствующая система будет
иметь вид:
|
|
(2.8) |
В процессе плавки асимметрия распределённой проводимости печи может изменяться. Именно асимметрия изменения сопротивлений позволяет определить значения электрических параметров плавильной печи.
Изложенная методика была опробована на реальных данных автоматического мониторинга процесса плавки, представленных на рис. 2.13- 2.14.
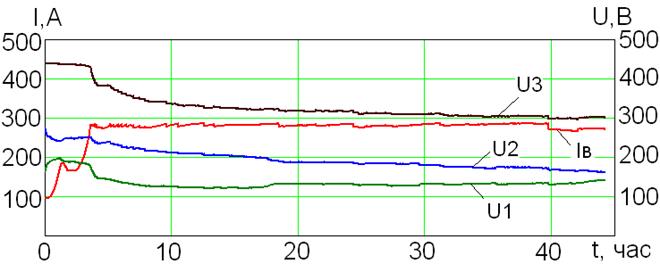
Рис. 2.13 − Экспериментальные данные U1,U2,U3,IВ
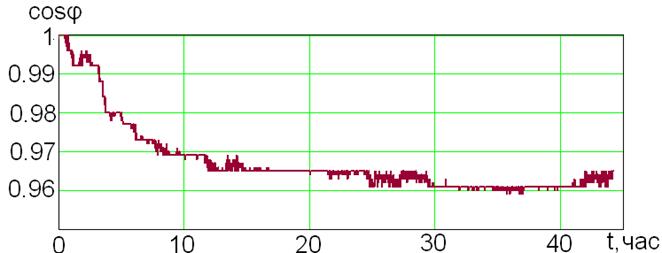
Рис. 2.14 − Экспериментальные данные коэффициента мощности
Приведенные данные соответствуют одному полному циклу плавильной кампании, проведённой на ОАО «Волжский абразивный завод» (печь №77, трансформатор №22 с 49 ступенями напряжения). Напряжение высоковольтной стороны в процессе плавки оставалось практически постоянным, изменяясь в диапазоне 10.4-10.5 кВ, и на графиках не показано.
Исходные данные для решения системы (2.6) выбирались с интервалом 10 минут. Всего использовалось 5 моментов времени для получения более точного решения. Решение проводилось методом Левенберга-Марквардта, являющимся квазиньютоновским методом (разновидностью градиентного метода) [27, 85]. Результаты приведены на рис. 2.15-2.17.
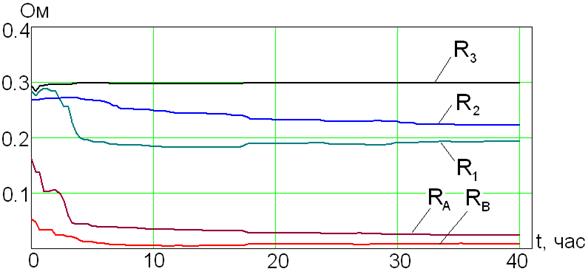
Рис. 2.15 - Активные сопротивления схемы замещения
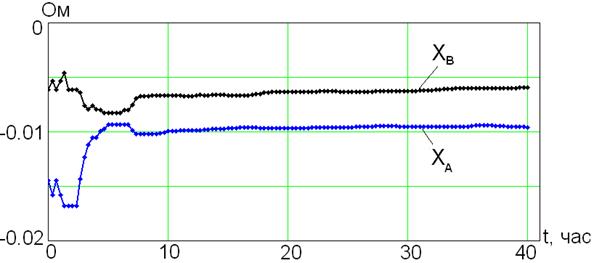
Рис. 2.16 - Реактивные сопротивления XA,XB
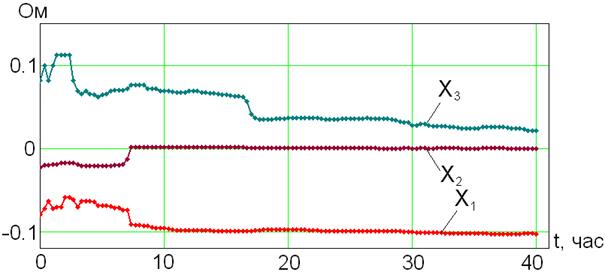
Рис. 2.17 - Реактивные сопротивления X1, X2, X3
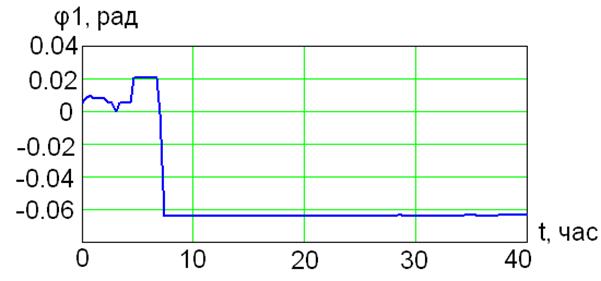
Рис. 2.18 - Фаза сдвига φ1
Численный метод Левенберга-Марквардта отличается тем, что для получения точного решения требуются хорошие начальные приближения [27]. При решении системы (2.8) задавались следующие начальные приближения:
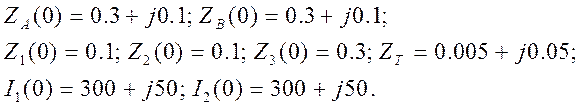
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.