Модернизация технологического процесса изготовления детали "корпус" с использованием прогрессивного оборудования и оснастки (Конструкторская часть дипломного проекта)

Конструкторская часть

4.1  Расчет и конструирование приспособления

1. Описание работы фрезерно-поворотного приспособления.

Предлагаемое приспособление устанавливается на ЛФ270Ф3 - полуавтомат вертикально-фрезерный с крестовым столом и с ЧПУ. Приспособление состоит из 3х кулачкового патрона соединенного со шпинделем, который находится в корпусе и вращение на который передаётся от храпового колеса, соединённого через фрикцион с червячной парой. Червяк находится на толкателе упирающемся в кулачек. От профиля кулачка зависит цикл поворота приспособления Основание крепится болтами на крестовом столе полуавтомата вертикально-фрезерного ЛФ270Ф3. Базируется с помощью шпонок.

Так в операции 010 обеспечивается поворот детали на 90^о.

2. Расчет силы резания при фрезеровании резьбы.

Используется фреза резьбовая Р6М5К5.

 

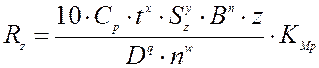
где   Z=6 – число зубьев фрезы;

        n=600 об/мин – частота вращения фрезы;

        D=20 мм – диаметр фрезы;

        B=16 мм – ширина фрезерования;

        =22,6 – поправочный коэффициент ([6], т.2, стр.296, табл.41);

        =0,15-0,30– подача фрезы на один зуб, мм/об ([6], т.2, стр.283, табл.33);

        x=0,86 – показатель степени ([6], т.2, стр.291, табл.41);

        y=0,72 – показатель степени ([6], т.2, стр.291, табл.41);

        q=0,86 – показатель степени ([6], т.2, стр.291, табл.41);

        w=0 – показатель степени ([6], т.2, стр.291, табл.41);

        n=1 – показатель степени ([6], т.2, стр.291, табл.41);

        t=0,6 мм – черновая обработка

        – поправочный коэффициент

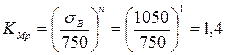
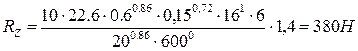
3. Необходимое условие зажима детали

F _ТР > R_Z,

Где F _ТР – сила трения детали в патроне

F _ТР = N*f,

N – сила реакции кулачков;

f = 0,23– коэффициент трения.

N = m*g,+ F,

F = 700Н– сила зажима заготовки в патроне,

m = 0,73 кг– масса заготовки в патроне,

g = 9,8м/с²– ускорение свободного падения

0,73*9,8+700>380

707>380

Необходимое условие выполняется

4. Достаточное условие зажима детали:

F_{CM /} S_CM = σ_CM < [σ_CM]

S_CM = L*π*R*3*φ/360 = 0.025*3.14*0.0495/2*3*30/360 = 4.85*10^-4 м² ,

F_CM  = m*g,+ F = 707Н- сила смятия

Где S_CM - площадь пятна контакта зажима на деталь;

L – длина закрепления;

R – радиус детали;

φ – угол раствора кулачка;

[σ _см ] = 600МПа– предельно допустимое напряжение на смятие

707/4,85*10^-4  = 1,46МПа <600МПа

Достаточное условие выполняется.

5. Расчет хода рейки

,

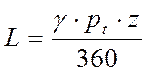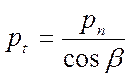- торцевой шаг

мм- нормальный шаг,

 = 15 – угол наклона зуба

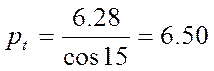мм

Z = 40 – число зубьев

γ = 90 – угол поворота колеса

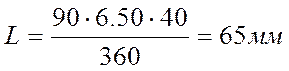
6. Расчёт механизма свободного хода

В процессе работы механизма свободного хода (МСХ храпового типа поверхности взаимодействия собачки и зубьев колеса  подвергаются ударным воздействиям. Тем не менее, при эксплуатации МСХ храповое колесо может работать при значительных угловых скоростях. Возникает необходимость определения предельных режимов движения, при которых деформация взаимодействующих поверхностей собачки и зубьев не превысила бы заданных значений и не вызывала бы их разрушение. Получить дифференциальное уравнение движения элементов МСХ можно, используя теорему об изменении главного вектора кинематического момента системы:

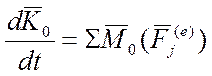
где  - вектор кинетического момента системы относительно неподвижной точки О;

 - радиус-вектор положения вектора количества движения точки;

 - вектор количества движения точки;

 - масса точки;

 - вектор скорости точки;

 - главный момент внешних сил, действующих на систему, относительно точки О;

 - вектор внешней силы, действующей на точку.

При исследовании динамики системы под действием удара учитывается только воздействие этой силы, а остальными силами пренебрегают.

После проектирования уравнения на ось вращения храпового колеса и интегрирования имеем:

где  -приведённый момент инерции системы (храповое колесо и ось вращения) относительно её оси вращения;

 - соответственно угловые скорости вращения системы после удара и до удара;

 - момент импульса внешних сил относительно оси вращения;

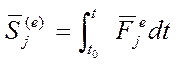 - вектор импульса внешних сил.

Если соотношение начальной и конечной угловых скоростей движения системы можно задать, например при ω=0, система после удара остановится, ω = ω₀/2 скорость вращения уменьшится вдвое, то очень сложно предложить величину промежутка времени, в течение которого произойдёт удар.

Следовательно, не удаётся решить задачу в коне виде.

Предлагается следующее решение.

Пусть в начальный момент храповое колесо имеет угловую скорость ω₀, а после взаимодействия с собачкой останавливается, то есть ω=0.

Поверхность взаимодействия зуба колеса с собачкой, нормально которой действует сила удара , а противодействует реакция зуба .