Элементарные звенья динамических систем. Временные характеристики звеньев (Практическое занятие № 3)

Практическое занятие 3

Элементарные звенья динамических систем.

Временные характеристики звеньев

3.1.  Теоретические положения

Классификация динамических звеньев определяется типом описывающих их дифференциальных уравнений.

Пусть x₁ – входная величина звена, а x₂ – выходная. Статическая характеристика любого линейного звена будет представлять собой прямую линию.

Для позиционных звеньев эта линия выражает зависимость между входной и выходной переменными величинами.

x₂=kx₁,

где k – коэффициент передачи звена.

Для интегрирующих звеньев линейная зависимость связывает производную выходной величины с первообразным входным сигналом:

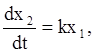
В установившемся положении

 

где  k – коэффициент передачи [S^-1].

Для   дифференцирующих звеньев получаем выражение

 

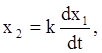
где коэффициент k[S] – имеет размерность времени.

Рассмотрим описание основных типов динамических звеньев, их дифференциальные уравнения и временные  характеристики.

a)  Позиционные динамические звенья

a.1. Безынерционное звено

Это звено описывается простым алгебраическим уравнением не только в статике, но и в динамике:

x₂=kx₁.

Его передаточная функция равна константе:

W(p)=W(jω)=k.

Этот тип динамических звеньев используется для описания широкого класса технических устройств ( быстродействующие электронные усилители редукторы без люфта и т.п.)

Переходная характеристика: h(t)=k 1(t).

Весовая функция: w(t)=k δ(t).

Амплитудно-фазовая частотная характеристика (АФЧХ) этого звена вырождена в точку, лежащую на расстоянии  k от начала координат на действительной оси

A(ω)=k=const,

φ (ω)=0=const.

a.2. Апериодическое звено первого порядка

Это звено можно описать дифференциальным уравнением вида:

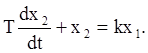
Передаточная функция: .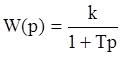

Такое описание характерно, например, для электродвигателя (с линейной механической характеристикой), R-C-цепи, газового ресивера, и т.д.

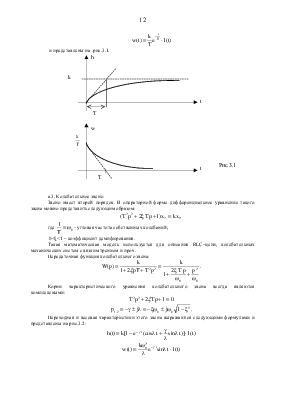
Временные характеристики звена описываются формулами:

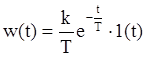
 и представлены на  рис.3.1.

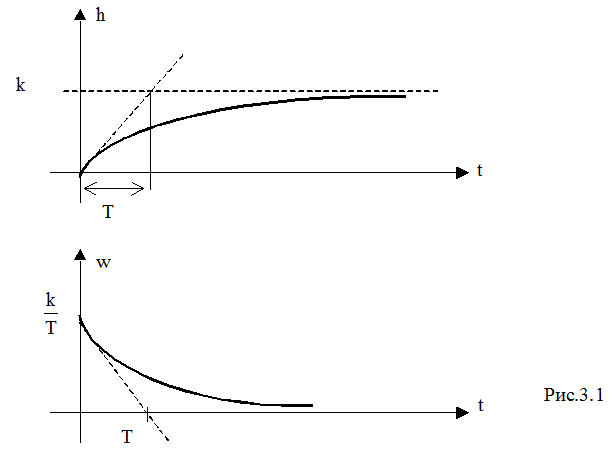
a.3. Колебательное звено

Звено имеет второй порядок. В операторной форме дифференциальное уравнение такого звена можно представить следующим образом:

где 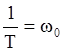- угловая частота собственных колебаний;

 0<ξ<1 – коэффициент демпфирования.

Такая математическая модель используется для описания RLC–цепи, колебательных механических систем с вязким трением и проч.

Передаточная функция колебательного звена:

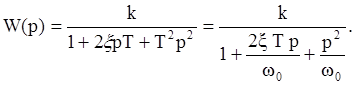
Корни характеристического уравнения колебательного звена всегда являются комплексными:

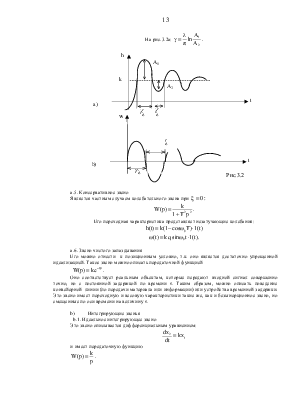
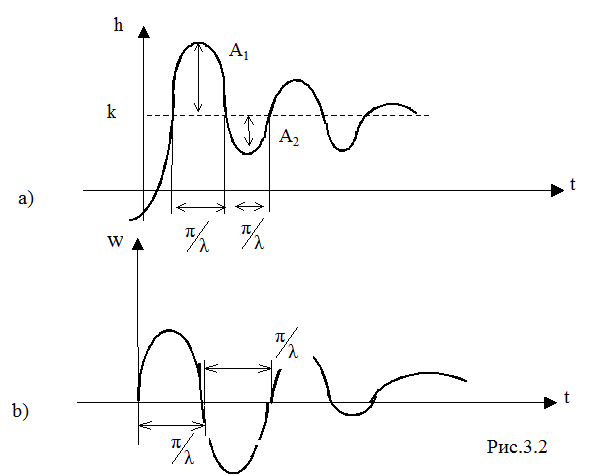
Переходная и весовая характеристики этого звена выражаются следующими формулами и представлены на рис.3.2:

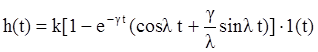
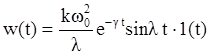
На рис.3.2a: .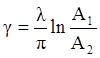

a.5. Консервативное звено

Является частным случаем колебательного звена при

.

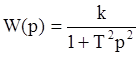Его переходная характеристика представляет незатухающие колебания:

a.6. Звено чистого запаздывания

Его можно отнести  к позиционным условно, т.к. оно является достаточно упрощенной идеализацией. Такое звено можно описать передаточной функцией

 .

Оно соответствует реальным объектам, которые передают входной сигнал совершенно точно, но с постоянной задержкой по времени τ. Таким образом, можно описать поведение конвейерной  линии (по передачи материала или информации) или устройства временной задержки. Это звено имеет переходную и весовую характеристики такие же, как и безынерционное звено, но смещенные по оси времени на величину τ.

b)  Интегрирующие звенья

  b.1. Идеальное интегрирующее звено

Это звено описывается дифференциальным уравнением:

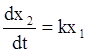
и имеет передаточную функцию

.

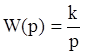Примеры интегрирующего звена: операционный усилитель с емкостью в обратной связи (рис.3.3), электродвигатель постоянного тока, если управляющее напряжение – входная величина, а угол поворота – выходная.

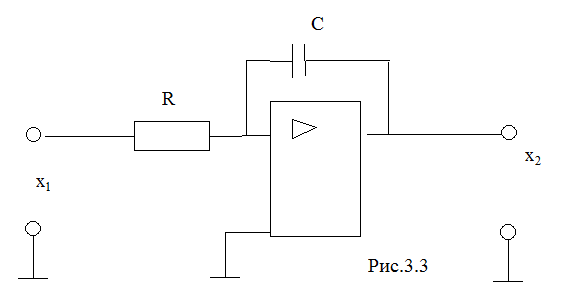
Переходная характеристика интегрирующего звена  - прямая, которая неограниченно возрастает во времени, угол ее наклона равен коэффициенту  k

h(t)=kt 1(t);

весовая функция

 w(t)=k 1(t)=const.

b.2. Интегрирующее звено с замедлением

Дифференциальное уравнение:

 .

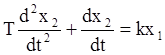Передаточная функция: ,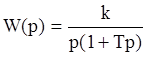

которую удобно представить последовательностью двух динамических звеньев:

;

;

.

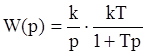b.3. Изодромное звено:

Дифференциальное уравнение:

 .

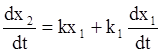Передаточная функция

.

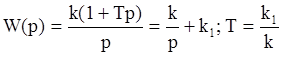Для изодромного звена:

.

c)  Дифференцирующие звенья

c.1. Идеальное дифференцирующее звено.

Дифференциальное уравнение

.

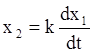Передаточная функция

Таким образом, это звено выдает производную от функции времени входного сигнала:

.

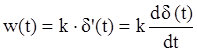Примером идеального дифференцирующего звена может служить тахогенератор, выходное напряжение которого пропорционально входной скорости вращения. Это звено имеет постоянную фазовую характеристику, равную ( ).

c.2. Дифференцирующее звено с замедлением

Дифференциальное уравнение: .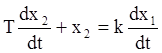

Передаточная функция: ,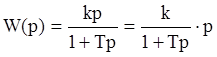

которая может быть представлена последовательным соединением идеального дифференцирующего и апериодического звеньев. Для этого звена

 

.

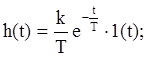
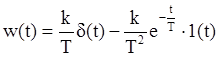Вообще говоря, любая сложная передаточная функция линейной системы может быть выражена через комбинацию следующего множества элементарных звеньев:

.

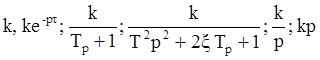3.2.  Практические задания

1)  Постройте переходную характеристику и АЧХ колебательного звена со следующими параметрами:  T=0.1 s, K=2, x=0.5;

2)  Постройте переходную характеристику и ФЧХ консервативного звена со следующими параметрами:    T=0.2 s, K=3.

3.3.   Контрольные  вопросы

1)  Поясните смысл введения понятия элементарного динамического звена.

2)  Назовите основные признаки, по которым классифицируются элементарные динамические звенья

3)  Приведите физические аналоги апериодического и интегрирующего звеньев.

4)  Какие общие свойства объединяют позиционные звенья?

5)  Назовите инерционные звенья второго порядка. Приведите их физические аналоги и характеристики

6)  Что такое передаточная функция звена?

7)  Как отличить звено с интегрированием от позиционных?

8)  Можно ли изобразить весовую характеристику идеального дифференцирующего звена?

9)  Запищите модель типа «Вход – состояние – выход» для двигателя постоянного тока, управляемого по якорной цепи (напряжение на обмотке возбуждения считать постоянным).

10)  Поясните различие между минимально-фазовыми и неминимально-фазовыми звеньями.