Моделирование гидродинамических процессов на основе теории подобия. Расчет процессов центрифугирования. Расчёт бетоносмесителя непрерывного действия

механики, экономисты, инженеры-проектировщики при выборе лучшего, оп­тимального варианта уже не могут только опираться на опыт, инженерную интуицию. Это объясняется усложнением технологических процессов, оби­лием и разнообразием взаимосвязей внутри каждого технологического пе­редела, необходимостью количественной оценки этих взаимосвязей. Тако­го рода оптимизационные проблемы возникают:

а) при управлении различными технологическими процессами, установ­ками, где необходимо достижение максимальной производительности при наилучшем качестве и минимальных затратах;

б) при проектировании разнообразных инженерных устройств, аппара­тов, приборов, схем, когда требуется подобрать такую комбинацию пара­метров, которая соответствовала бы наивысшим эксплуатационным характе­ристикам проектируемого аппарата;

в) при создании новых образцов строительной продукции, материалов, смесей, при синтезе веществ, обладающих наилучшими свойствами (напри­мер, максимальной прочностью, если речь идет о строительных материа­лах).

К оптимизационным сводятся многие задачи чисто вычислительного ха­рактера, например, численное построение плана эксперимента, оптималь­ного в соответствии с выбранный критерием.

1. Моделирование гидродинамических процессов на основе теории подобия.

Для экспериментального изучения в лабораторных условиях некоторого производственного процесса изготовлена геометрическая модель производственного аппарата в масштабе 1:10, в производственном аппарате рабочее вещество - горячий воздух c температурой 100°С при атмосферном давлении, движущейся со скоростью 3 м/с. В лабораторной модели предполагается  применять в качестве рабочего вещества воздух с температурой 22°С. Определить возможно ли получение при этих условиях полного гидродинамического подобия промышленного аппарата и модели. Какова должна быть скорость воздуха в модели. При необходимости назначить модель с полным подобием.

Для решения задачи используются критерии Рейнольдса и Фруда:

;

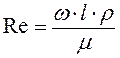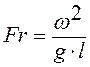
Для соблюдения полного гидродинамического подобия при подобных граничных условиях необходимо равенство критериев подобия модели в реальном аппарате

,                                        

 ,                                                    

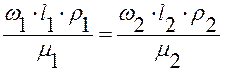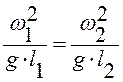где ω₁ и ω₂ – скорости в аппарате и модели;

 l₁ и l₂ – масштаб размера аппарата и модели;

 ρ₁ и ρ₂ – плотность рабочего вещества;

 μ₁ и μ₂ – вязкость вещества.

Из таблицы берем значение плотности рабочего вещества (воздуха) ρ_в при 0°С ρ_о=1,29 кг/м³. Делаем корректировку на температуру:

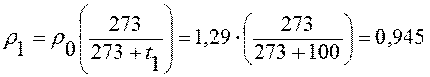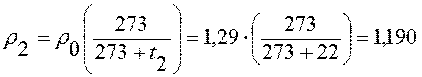 кг/м³

 кг/м³

Необходимо найти вязкость воздуха по номограмме:

Т. к. соотношение 1:20, то l₂=0,05l₁

Скорость воздуха в модели по критерию Рейнольдса:

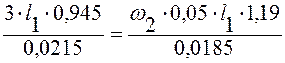
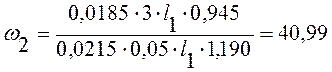м/с

Согласно 3-ей теории подобия необходимое и достаточное условие будет выполняться, если скорость модели будет 40 м/с.

Скорость воздуха в модели по критерию Фруда:

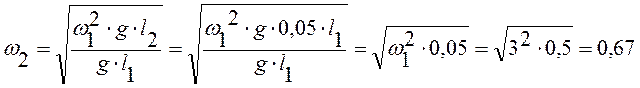 м/с

Вывод: Получение полного гидродинамического подобия для принятой модели (1:20, t₂=22°С, воздух) не возможно. Следует изменить модель.

Новая модель №2.

Изменим температуру в модели t₂=-22°С и возьмём соотношение 1:1,55. В связи с изменившимися параметрами, корректируем плотность:

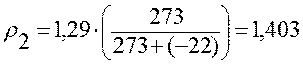 кг/м³

Динамический коэффициент вязкости в новой модели определяем