


Лекция 7
Решение дифференциальных уравнений систем автоматического управления
Принцип суперпозиции
план
1. Сокращенная форма записи дифференциальных уравнений систем автоматического управления
2. Принцип суперпозиции
3. Установившиеся и переходные процессы
4. Свободные движения системы. Нулевые, простые и кратные корни
5. Вынужденные движения системы
Когда мы используем дифференциальный оператор Лапласа 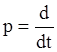 дифференциальной уравнение системы можно
записать в форме полинома :
дифференциальной уравнение системы можно
записать в форме полинома :
D(p)x(t)=Q(p)g(t)+N(p)f(t) (1)
где D(p),Q(p) и N(p) – полиномы от р.
В замкнутых системах в качестве общей фазовой координаты обычно используется ошибка x(t) , т.e. разность между задающим воздействием и сигналом главной обратной связи :
x(t) = g(t) – xfb(t).
D(p) выражает свободные движения системы, когда задающее (управляющее) воздействие g(t) º0 и возмущающее воздействие f(t) º0. Он называется характеристическим полиномом системы:
D(p)=anpn+anpn-1+…+a1p+a0
Q(p) выражает влияние управляющего воздействия на рассматриваемую систему (на сигнал x(t)).
Q(p)=cmpm+…+c1p+c0
N(p) выражает влияние возмущающего воздействия f(t) на сигнал ошибки x(t). Если линейная система одновременно испытывает влияние нескольких внешних сигналов (возмущений, управляющих)., можно выразить результат их воздействия на систему как сумму результатов отдельных воздействий каждого отдельного внешнего сигнала. Эта особенность линейных систем называется принципом суперпозиции. Он может быть легко доказан с применением теоремы линейности. (рис.1)
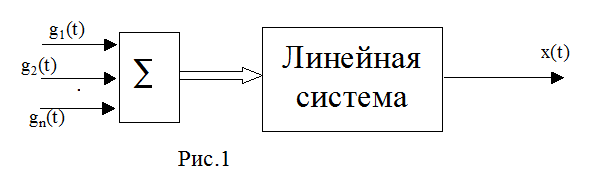
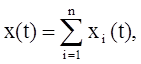
где xi(t), ![]() -частные
результаты внешних воздействий gi(t),
-частные
результаты внешних воздействий gi(t), ![]()
Эта особенность справедлива и для возмущающих воздействий fk(t). Если fk(t) ¹0 , но характеристический многочлен Nk(p)=0, то система будет называться инвариантной относительно данного сигнала fk(t).
Решение любого линейного дифференциального уравнения состоит из общего однородного решения (определяемого левой частью) и частного неоднородного решения (определяемого как правой так и левой частями). Таким образом все решение дифференциального уравнения делится на две части, влияющих на состояние автоматической системы независимо от другого.
Найдем в первую очередь свободные движения системы. Можно выделить несколько частных случаев свободных движений системы в соответствии с распределением корней D(p).
Как известно, уравнение
имеет общий вид решения
![]()
где ![]() причем для некоторых i
может быть ai=0 или bi=0
причем для некоторых i
может быть ai=0 или bi=0
Если система имеет все корни характеристического
полинома с bi=0 и ai<0, то
свободные движения системы имеют характер затухающего апериодического процесса ![]() . Система устойчива. Если bi=0 и хотя
бы один из ai<0, то
переходный процесс также будет апериодических (экспоненциальным) с
неограниченным возрастанием сигнала. Система неустойчива
. Система устойчива. Если bi=0 и хотя
бы один из ai<0, то
переходный процесс также будет апериодических (экспоненциальным) с
неограниченным возрастанием сигнала. Система неустойчива ![]() . Если характеристический полином имеет
корни с ненулевой мнимой частью, то переходный процесс системы будет иметь
колебательную составляющую. Процесс в целом может быть устойчивым("aI<0)
или неустойчивым (неограниченно возрастающим) в соответствии со знаком
действительной части корней. Свободные движения системы будут затухать, если
все ai<0.
Пара чисто мнимых корней
. Если характеристический полином имеет
корни с ненулевой мнимой частью, то переходный процесс системы будет иметь
колебательную составляющую. Процесс в целом может быть устойчивым("aI<0)
или неустойчивым (неограниченно возрастающим) в соответствии со знаком
действительной части корней. Свободные движения системы будут затухать, если
все ai<0.
Пара чисто мнимых корней ![]() дает в решении
незатухающую колебательную составляющую, которая будет присутствовать не только
в переходном, но и в установившемся процессе. Такая система находится на
колебательной границе устойчивости.
дает в решении
незатухающую колебательную составляющую, которая будет присутствовать не только
в переходном, но и в установившемся процессе. Такая система находится на
колебательной границе устойчивости.
Если D(p) имеет нулевой корень, то она находится на апериодической границе устойчивости. Свободные движения такой системы могут окончиться при любой установившейся величине переменной x(t).
Вообще говоря, переходный процесс определен только для устойчивых систем. Этот термин означает время от начала воздействия некоторого сигнала до достижения устойчивого состояния по всем фазовым координатам (исключая случай устойчивых колебаний). Когда переходный процесс закончен, начинается установившийся процесс (состояние). Когда в системе присутствует внешнее воздействие, дя получения установившегося процесса управляющий или возмущающий сигнал должен быть постоянным.
Рассмотрим более подробно решение уравнения (1) при
условиях g(t) ¹0 и x(0) ¹0, ![]() …. .
…. .
В преобразовании Лапласа:
(anpn+an-1pn-1+…+a1p+a0)x(p)-x(-0)(anpn-1+an-1pn-2+…+a2p+a1)-
-![]() (-0)(anpn-2+an-1pn-3+…+a3p+a2)-…-x(n-2)(-0)(anp+an-1)-x(n-1)(-0)an=
(-0)(anpn-2+an-1pn-3+…+a3p+a2)-…-x(n-2)(-0)(anp+an-1)-x(n-1)(-0)an=
=(bmpm+bm-1pm-1+…+b1p+b0)G(p)
или
D(p)X(p)-DN(p)=Q(p)G(p)
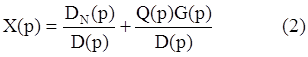
Пусть 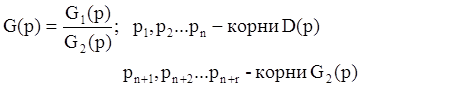
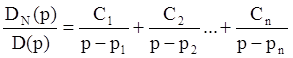
В последнем выражении каждый действительный корень pi соответствует действительному Ci, а комплексный рi соответствует комплексному коэффициенту Ci
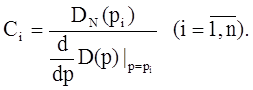
Вторая часть выражения (2) соответствует вынужденным движениям системы:
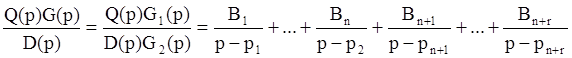
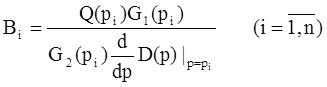
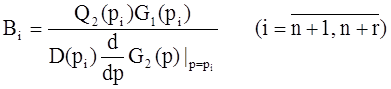
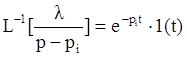
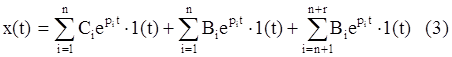
Первая сумма в (3)
соответствует свободным движениям системы (собственным движениям) (см. выше).
Вторая часть зависит как от свойств системы, так и от внешнего сигнала. Эту
часть обычно называют сопровождающими движениями. При ![]() поведение
этих движений такое же, как и у собственных.
поведение
этих движений такое же, как и у собственных.
В последней сумме в (3) характер каждого слагаемого определяется корнями G2(p) (внешнего воздействия). Вид этих движений подобен внешнему воздействию. Например:
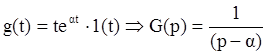
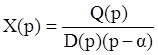
Мы имеем одну
вынужденную компоненту в (3): ![]() соответствующую виду
функции g(t).
соответствующую виду
функции g(t).
Наконец рассмотрим кратные корни D(p). Пусть порядок корня p1 будет равен числу r£n.
Первая сумма (2) в этом случае будет иметь вид:
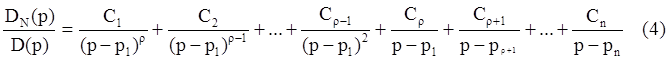
тогда
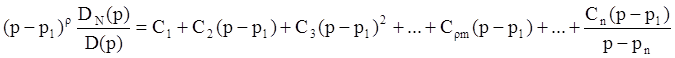
Затем можно вычислить Ci как было указано выше:
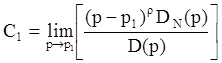
……………………………………..
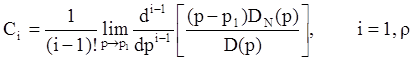
Выполняя обратное преобразование Лапласа для (4) в соответствии с таблицей 2 (из предыдущей лекции) можно получить для первого слагаемого в (4) соответствующий оригинал, пропорциональный величине t r-1.
Следовательно: 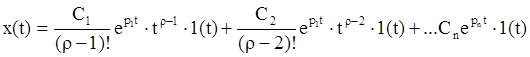
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.