Расчет линейных цепей однофазного синусоидального тока

2. Расчет линейных цепей

однофазного синусоидального тока

2.1. Основные понятия и определения

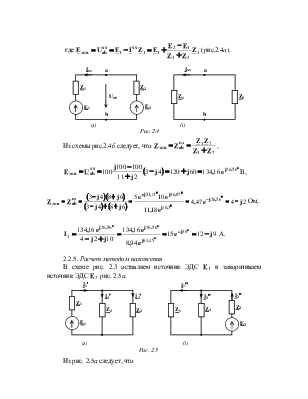
Электрической цепью синусоидального тока называется цепь, в которой действуют ЭДС, напряжения и токи, изменяющиеся во времени по синусоидальному закону.

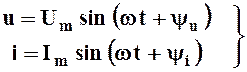.                                     (2.1)

Их временные диаграммы имеют вид рис. 2.1.

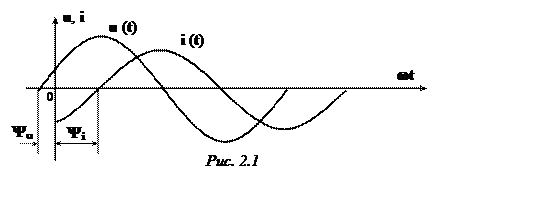Синусоидальные токи, напряжения и ЭДС – величины периодические. Они характеризуются:

- мгновенными значениями u, i, e, т.е., значениями в рассматриваемый момент времени (например, при , );   

- периодом Т, с , т.е., промежутком времени, по истечении которого синусоидальный ток (напряжение, ЭДС) принимает одно и то же мгновенное значение , где n- целое число;

- частотой f, Гц , т.е., числом полных изменений периодической величины в течение одной секунды

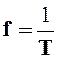;                                                (2.2)

- амплитудой (, , ), т.е.,  максимальным значением синусоидальной величины;

- фазой (фазовым углом), рад, т.е., аргументом синусоидальной величины, например, для тока

;                                            (2.3)

- начальной фазой Y, рад, т.е., значением фазы (аргумента) в момент времени . Начальная фаза считается положительной, если при  мгновенное значение синусоидальной величины положительно, и, наоборот, отрицательной, если в тот же момент времени мгновенное значение синусоидальной величины отрицательно. На временных диаграммах положительную начальную фазу откладывают влево, а отрицательную – вправо от начала координат (на рис.2.1 , а );

- угловой частотой w, рад/с, т.е., скоростью изменения фазы (  фазового угла)

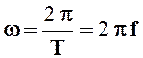;                                          (2.4)

- сдвигом фаз j, рад, т.е., разностью фаз двух синусоидальных величин. Сдвиг фаз между напряжением  u и током iобозначают буквой j и, в соответствии с определением,

;                      (2.5)

- действующим значением тока (напряжения, ЭДС), т.е., среднеквадратичным значением этих величин за время, равное периоду

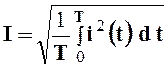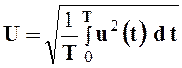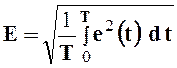 ; ; .         (2.6)

Подставив в (2.6) выражения (2.1) и произведя интегрирование, можно показать, что между действующими и амплитудными значениями синусоидальных величин справедливы соотношения

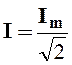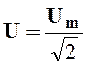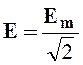; ; .                                 (2.7)

Действующие значения тока, напряжения и ЭДС не зависят от времени и являются эквивалентными некоторым постоянным значениям тока I, напряжения U и ЭДС E, которые производят в электрической цепи такое же тепловое действие, что и переменные ток i, напряжение u и ЭДС e за одинаковый промежуток времени;

- средним значением периодического тока, ЭДС и напряжения

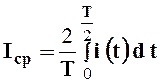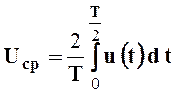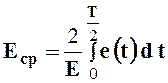; ; .           (2.8)

Для синусоидальных токов, напряжений и ЭДС из (2.8) следует, что

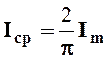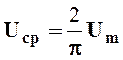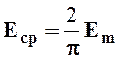; ; .                          (2.9)

2.2. Методы расчета сложных линейных электрических цепей синусоидального тока

Расчет сложных электрических цепей синусоидального тока производят теми же методами, что и расчет сложных электрических цепей постоянного тока. Разница заключается в том, что уравнения составляются для комплексных токов, напряжений и ЭДС, в которых сопротивление R, проводимость G и потенциалы jзаменяют комплексными сопротивлениями Z, проводимостями Y и потенциалами j  узлов.

  При расчете цепей с одним источником ЭДС с применением комплексных чисел широко используется метод эквивалентных преобразований. При этом:

- в случае последовательного соединения нескольких комплексных сопротивлений это соединение можно заменить эквивалентным комплексным сопротивлением

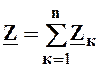,                                              (2.10)

- в случае параллельного соединения нескольких ветвей, заданных комплексными проводимостями , это соединение можно заменить одной эквивалентной комплексной проводимостью

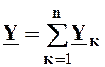,                                             (2.11)

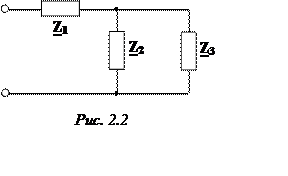
- в случае смешанного (последовательно-параллельного) соединения трех ветвей с сопротивлениями ,  и  рис. 2.2, это соединение может быть заменено эквивалентным комплексным сопротивлением

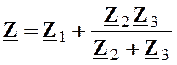.                                         (2.12)

Расчет сложной цепи переменного синусоидального тока часто упрощается, если применить преобразование треугольника сопротивлений в эквивалентную звезду и наоборот – звезды в треугольник. Для этого в формулах для цепей постоянного тока следует заменить резистивные сопротивления  на комплексные сопротивления [1].

Методы расчета цепей синусоидального тока с несколькими источниками ЭДС в символической (комплексной) форме проиллюстрируем на примере расчета цепи рис. 2.3.

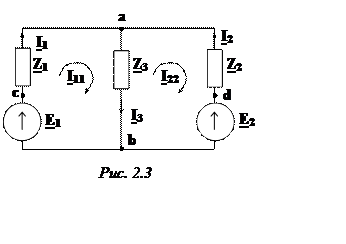Дано:

В;  В;

 Ом;  Ом;

Ом

                                                                 Требуется рассчитать токи во всех

                                                                  ветвях различными методами.

2.2.1. Непосредственное применение законов Кирхгофа (МЗК)

В схеме два узлаa и b и три ветви. Составляем одно уравнение по первому закону Кирхгофа и два уравнения по второму закону Кирхгофа, задавшись направлением обхода в каждом из независимых контуров. В результате получим систему уравнений:

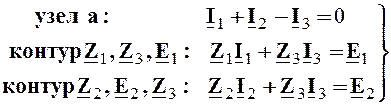 или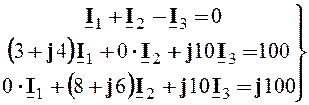

Решив систему уравнений, находим комплексные токи в ветвях:

А;   А; А.

Записываем выражения для мгновенных токов:

 А;  А;

 А.

2.2.2. Расчет методом контурных токов (МКТ)

В каждом из независимых контуров рис.2.3 указываем дугами контурные токи  и  и записываем систему уравнений по второму закону Кирхгофа для контурных токов

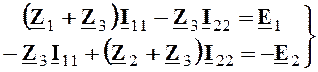 или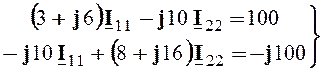

Решив эту систему относительно контурных токов , , определяем токи в ветвях:

 А;  А;

 А.

2.2.3. Расчет методом двух узлов (МУП)

Поскольку в рассматриваемой схеме только два узла, то метод узловых потенциалов для схемы рис.2.3 сводится к методу двух узло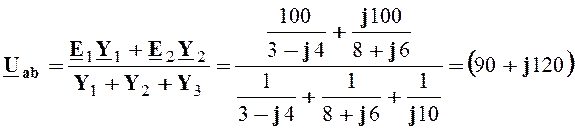в:

 В.

Токи в каждой из ветвей определяем по обобщенному закону Ома в символической форме: