Лабораторная работа N 1.3
Исследование сложных линейных цепей постоянного тока с несколькими источниками ЭДС
Цель работы:
· освоить и экспериментально проверить расчет линейных цепей постоянного тока методом наложения и эквивалентного генератора;
· освоить методику расчета, измерения и построения потенциальной диаграммы.
1. Краткие теоретические сведения
1.1. Метод наложения полагает, что каждая ЭДС вызывает в отдельных ветвях электрической цепи свои (частичные) токи независимо от действия всех остальных ЭДС, включенных в эту же цепь. Это позволяет найти ток в любой ветви, как алгебраическую сумму токов, возникающих в этой ветви при действии каждой ЭДС отдельно. Так, расчет токораспределения в электрической цепи рис.3.1а методом наложения сводится к нахождению токов в двух более простых цепях с ЭДС Е1 (рис.3.1б) и ЭДС Е2 (рис.3.1в) при сохранении в них прежних значений внешних и внутренних сопротивлений.
В электрической цепи рис.3.1б токи в ветвях определяются из выражений
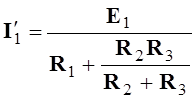 ;
; 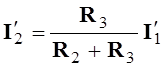 ;
; 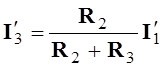 .
.
Аналогично в электрической цепи рис.3.1в токи в ветвях определяются из выражений
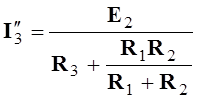 ;
; 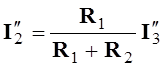 ;
; 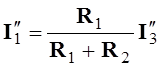 .
.
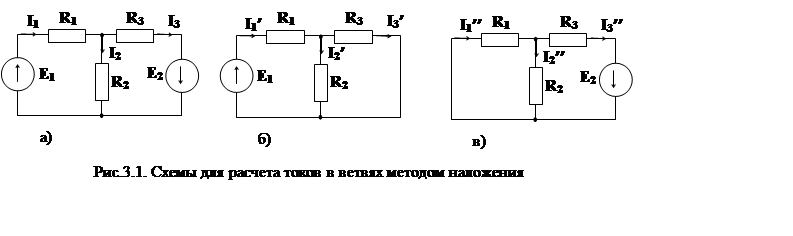
Наложение
токов ![]() ,
, ![]() ,
, ![]() на токи
на токи ![]() ,
, ![]() ,
, ![]() , с
учетом их направлений, позволяет найти действительные токи в ветвях исходной
схемы рис.3.1а
, с
учетом их направлений, позволяет найти действительные токи в ветвях исходной
схемы рис.3.1а
![]() ;
; ![]() ;
; ![]() .
.
1.2.
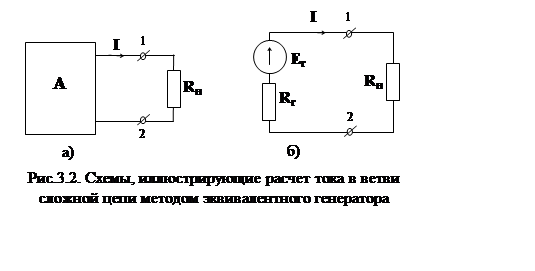
Метод эквивалентного генератора позволяет определить ток в одной из
ветвей разветвленной электрической цепи. При этом ветвь можно рассматривать как
нагрузку, подключенную в точках 1 и 2 рис.3.2а к своеобразному генератору,
которым является остальная сложная электрическая цепь. Такой условный
генератор, обладающий некоторой эквивалентной ЭДС ![]() и
некоторым эквивалентным внутренним сопротивлением
и
некоторым эквивалентным внутренним сопротивлением ![]() , принято
называть эквивалентным генератором или активным (содержащим источники ЭДС)
двухполюсником.
, принято
называть эквивалентным генератором или активным (содержащим источники ЭДС)
двухполюсником.
 Применительно к
случаю, когда выделенная ветвь является пассивной (рис.3.2), ток в ней
находится по соотношению
Применительно к
случаю, когда выделенная ветвь является пассивной (рис.3.2), ток в ней
находится по соотношению  .
.
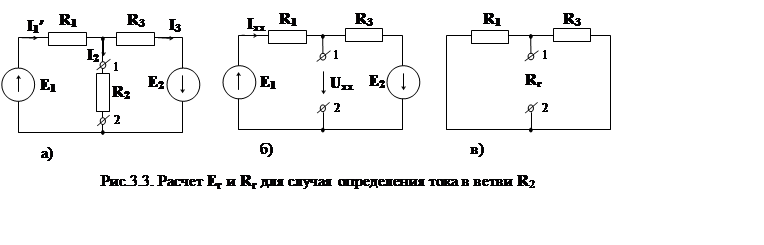
ЭДС ![]() равна разности потенциалов между зажимами 1 и 2
рис.3.3б при условии, что рассматриваемая ветвь
равна разности потенциалов между зажимами 1 и 2
рис.3.3б при условии, что рассматриваемая ветвь ![]() разомкнута,
т.е.
разомкнута,
т.е.
![]() .
.
Так
как 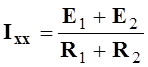 , то
, то 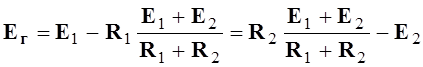 .
.
Сопротивление ![]() равно
сопротивлению всей цепи между зажимами 1 и 2 при отключенной нагрузке
равно
сопротивлению всей цепи между зажимами 1 и 2 при отключенной нагрузке ![]() и равенстве нулю всех имеющихся в цепи
источников ЭДС рис.3.3в
и равенстве нулю всех имеющихся в цепи
источников ЭДС рис.3.3в 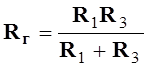 .
.
Экспериментально параметры ![]() и
и ![]() определяются
по соотношениям
определяются
по соотношениям
![]() и
и 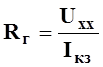 ,
,
где ![]() -
напряжение на зажимах 1 и 2 рис.3.3б, при
-
напряжение на зажимах 1 и 2 рис.3.3б, при ![]() (измеряется
вольтметром, подключаемым к зажимам 1 и 2 при отключенной нагрузке
(измеряется
вольтметром, подключаемым к зажимам 1 и 2 при отключенной нагрузке ![]() );
);
![]() - ток в ветви
- ток в ветви ![]() при
при ![]() (измеряется амперметром, включенным между
зажимами 1 и 2 вместо
(измеряется амперметром, включенным между
зажимами 1 и 2 вместо ![]() ).
).
1.3. Под потенциальной диаграммой понимают график распределения потенциала вдоль какого-либо участка цепи или замкнутого контура, в зависимости от суммарного сопротивления от базовой точки (потенциал которой принимается равным нулю) до каждой характерной точки заданного контура. При этом по оси абсцисс откладываются суммарные сопротивления, а по оси ординат – потенциалы.
Для построения диаграммы определяется сумма
сопротивлений всех резисторов, входящих в заданный контур, и выбирается масштаб
![]() (Ом/мм) по оси абсцисс. Далее
рассчитываются или измеряются вольтметром постоянного тока (чувствительным к
полярности) потенциалы всех точек контура по отношению к базовой точке и
выбирается масштаб
(Ом/мм) по оси абсцисс. Далее
рассчитываются или измеряются вольтметром постоянного тока (чувствительным к
полярности) потенциалы всех точек контура по отношению к базовой точке и
выбирается масштаб ![]() (В/мм).
(В/мм).
![]() ,
,
где ![]() -
потенциал последующей точки контура;
-
потенциал последующей точки контура;
![]() - потенциал предыдущей точки контура;
- потенциал предыдущей точки контура;
Е и R – ЭДС источника напряжения или электрическое сопротивление резистора, включенного между точками 1 и 2;
I – величина тока, протекающего через резистор R.
Знак перед ЭДС берется положительный, если направление
ЭДС совпадает с направлением обхода контура, а знак падения напряжения ![]() берется положительным, если направление
тока I через
резистор Rвстречно
направлению обхода.
берется положительным, если направление
тока I через
резистор Rвстречно
направлению обхода.
Для измерения потенциалов всех точек контура вольтметром, отрицательный зажим вольтметра соединяется с базовой точкой, а положительным поочередно касаются к остальным точкам контура. При этом переключатель полярности вольтметра должен быть установлен на знак “+”. Если при этом стрелка вольтметра отклонится вправо, то потенциал больше нуля (т.е. положителен), а если влево – то потенциал меньше нуля (отрицателен). Для измерения вольтметром отрицательного потенциала необходимо переключатель полярности установить на знак “-”. Результаты расчетов или (и) измерений заносятся в таблицу (см.таблицу 3.3) и строится диаграмма рис.3.4.
Вертикальные участки диаграммы отвечают переходам через идеальные источники ЭДС.
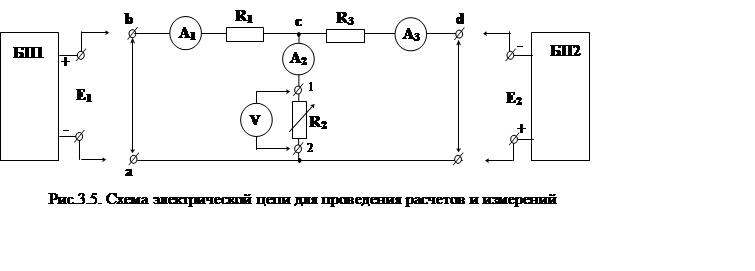
1.4. Расчеты и экспериментальные измерения в данной работе приводятся применительно к схеме рис.3.5.
 |
2. Задание, выполняемое при домашней подготовке
2.1. По конспекту лекций, рекомендуемой литературе [1-4] и разделу 1 данной работы освоить методы анализа линейных электрических цепей с несколькими источниками ЭДС (метод наложения и эквивалентного генератора).
2.2.
По исходным данным, полученным от преподавателя на предыдущем занятии,
рассчитать токи в ветвях схемы рис.3.5 для случая, когда вместо перемычек
включены источники ЭДС ![]() и
и ![]() с
указанной на схеме полярностью методом наложения, а также ток
с
указанной на схеме полярностью методом наложения, а также ток ![]() - методом эквивалентного генератора.
Результаты расчетов занести в таблицы 1 и 2.
- методом эквивалентного генератора.
Результаты расчетов занести в таблицы 1 и 2.
2.3. Заготовить отчет по требованиям раздела 5.
3. Лабораторное задание
3.1. Произвести проверку метода наложения, для чего:
· Собрать схему рис.3.5, включив между точками a и b вместо перемычки источник ЭДС E1, соблюдая полярность.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.