Исследование линейной однофазной электрической цепи синусоидального тока с параллельным соединением элементов (Лабораторная работа № 1.6)

Лабораторная работа N 1.6

Исследование линейной однофазной электрической цепи                     синусоидального тока с параллельным соединением элементов

Цель работы:

·  исследовать электрическое состояние линейной цепи синусоидального тока с параллельным соединением различных приемников;

·  научиться вычислять параметры электрической цепи и строить векторные диаграммы, треугольники токов, проводимостей и мощностей по опытным данным;

·  исследовать явление резонанса токов и определить параметры колебательного контура.

1. Краткие теоретические сведения

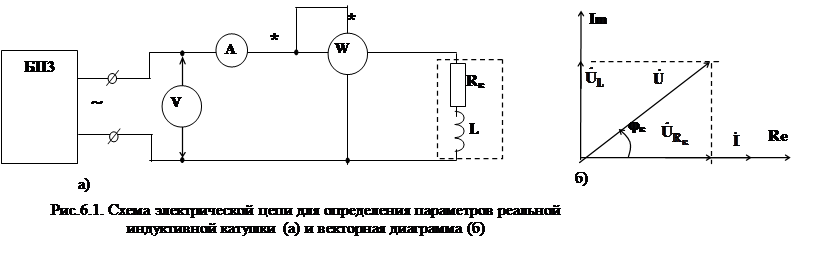
1.1. На рис.6.1а приведена электрическая цепь, содержащая реальную индуктивную катушку с параметрами R_к и L.

 

Величина (действующее значение) тока в такой цепи равно

,

где U – действующее значение напряжения на зажимах цепи;

               y – полная проводимость всей цепи (модуль комплекса входной проводимости цепи ).

Измерив экспериментально величины U, I и P, можно определить параметры катушки

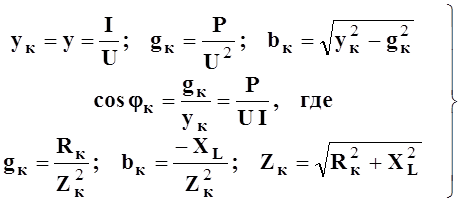             (6.1)

Записав закон Ома в символической (комплексной) форме, получим

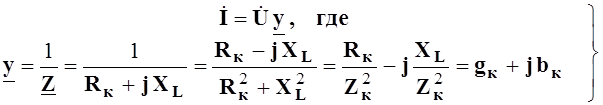     (6.2)

Из (6.2) следуют соотношения (6.1), причем проводимость .

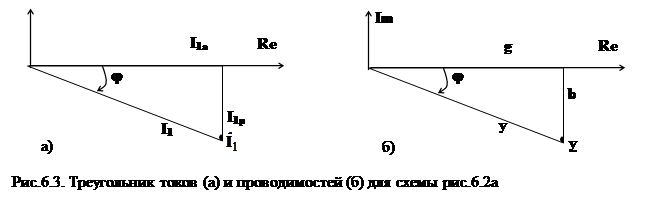
Векторная диаграмма напряжений и токов для схемы рия.6.1а приведена на рис.6.1б. Она строится методом “засечек”.

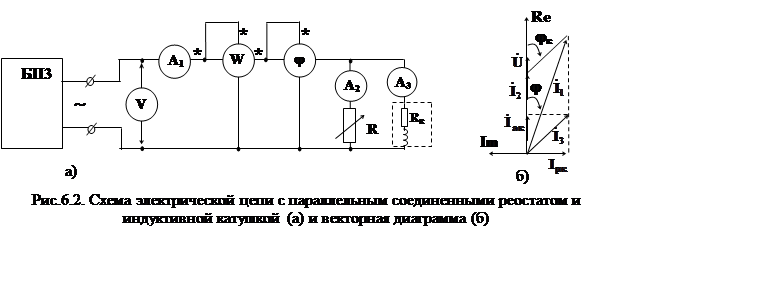1.2. На рис.6.2а приведена электрическая цепь, составленная параллельным соединением реальной индуктивной катушки с параметрами R_к, Lи реостата с регулируемым электрическим сопротивлением R.

Величина тока I₁ в неразветвленной части цепи равна

,

где U – действующее напряжение на входных зажимах цепи;

y - полная входная проводимость цепи.

Токи в ветвях равны

 и , где y₂ и y₃ – полные проводимости ветвей.

Измерив  с помощью приборов величины U, I₁, P, I₂, I₃ , можно определить параметры всей цепи и катушки

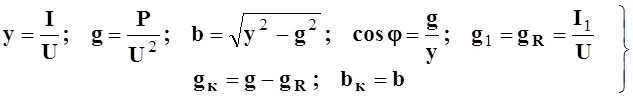     (6.3)

Записав уравнение по первому закону Кирхгофа в символической (комплексной) форме, получим

, где  и, следовательно, входная комплексная проводимость цепи y равна сумме комплексных проводимостей всех параллельно включенных ветвей

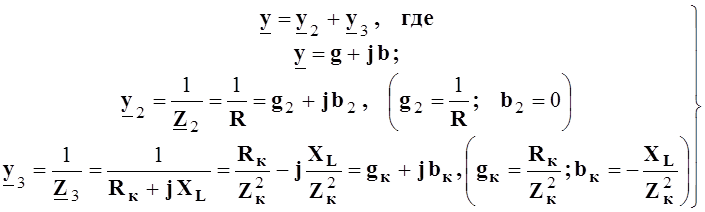(6.4)

Из соотношений (6.4), с учетом закона Ома для действующих U и Iи треугольника проводимостей, следуют соотношения (6.3).

Im

На рис.6.2б приведена векторная диаграмма напряжений и токов, а на рис.6.3а и 6.3б – треугольники токов и проводимостей.

 

На рис.6.4а приведена электрическая цепь, составленная параллельным соединением реостата R и конденсатора С.

 

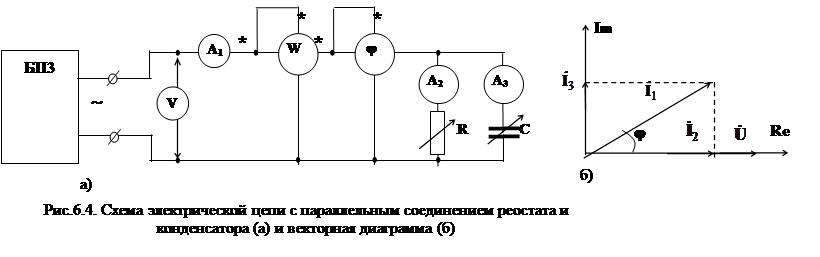
Параметры этой цепи можно определить по показаниям приборов аналогично предыдущим случаям.

На рис.6.4б приведена векторная диаграмма для этой цепи, а на рис.6.5а,б – треугольник токов и проводимостей.

 

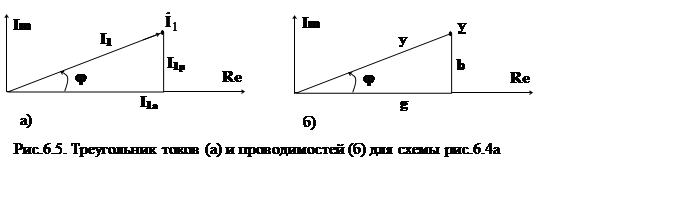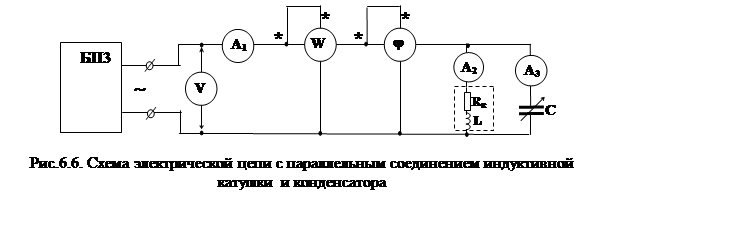
На рис.6.6 приведена схема электрической цепи из параллельно включенных индуктивной катушки и конденсатора.

 

Как и для схемы рис.6.2, первый закон Кирхгофа в символической форме имеет вид

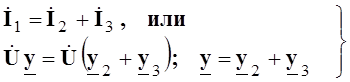                         (6.5)

Следовательно, комплекс  входной проводимости цепи равен сумме комплексных проводимостей параллельных ветвей.

При этом, по закону Ома в символической форме

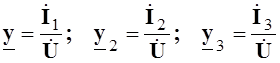.                             (6.6)

При построении векторных диаграмм рис.6.7 начальную фазу комплекса напряжения  на входе цепи принимаем равной нулю (). На рис.6.7а построена диаграмма для случая, когда разность фаз j между напряжением на входе и током  в неразветвленной части цепи больше нуля (). Этот случай имеет место, когда .

Так как сопротивление второй ветви активно-индуктивное, то ток  отстает по фазе от на угол 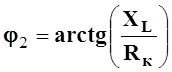. Ток третьей ветви опережает по фазе напряжение на угол . При этом, вектор тока  равен векторной сумме векторов  и , согласно первому закону Кирхгофа.

 

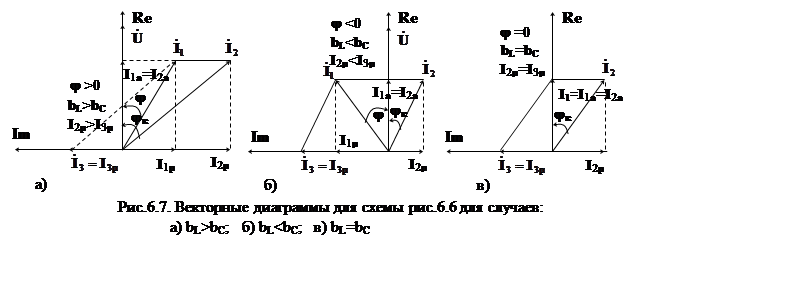
Режим, при котором в цепи, содержащей параллельные ветви с индуктивным и емкостным элементами, ток  в неразветвленном участке цепи совпадает по фазе с напряжением  на входных зажимах этой цепи, называют резонансом токов.

Как следует из рис.6.7в, резонансу токов отвечает равенство модулей реактивных составляющих токов ветвей

.                                            (6.7)

Так как  и , то условие резонанса можно записать в виде

,                                             (6.8)

или

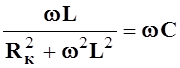.                                  (6.9)

При заданных параметрах , L и С, условие резонанса может быть достигнуто на определенной частоте , называемой резонансной

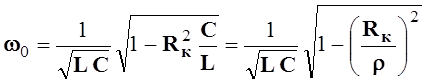,           (6.10)

где 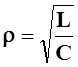 - характеристическое сопротивление контура.

Из (6.10) следует, что резонанс возможен в цепи рис.6.6, если сопротивление .

При резонансе токов полная проводимость цепи рис.6.6 минимальная (), т.е., входное сопротивление достигает максимума, вследствие чего ток  будет минимальный, что является одним из признаков настройки цепи в резонанс. При этом очевидно, что фазометр покажет значение .

Отношение реактивных составляющих токов в ветвях к току  при резонансе токов называется добротностью параллельного колебательного контура q

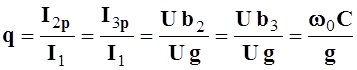.                 (6.11)

Так как при резонансе токов  (), то активная мощность равна полной мощности цепи, т.е.,

.                         (6.12)

Реактивная мощность Qпри резонансе токов равна нулю

.                  (6.13)

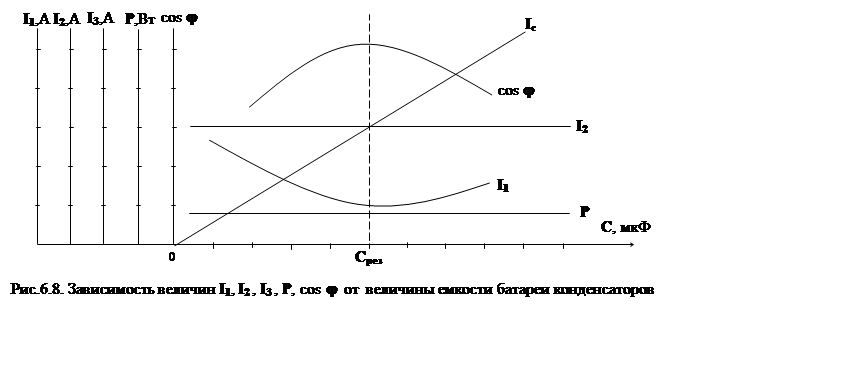
Если в схеме рис.6.6 изменять величину емкости С, то величины , , , Pи cosj будут изменяться по рис.6.8.

 

2. Задание, выполняемое при домашней подготовке

2.1. По конспекту лекций, рекомендуемой литературе и разделу 1 данной работы изучить особенности анализа электрических процессов в линейных цепях однофазного синусоидального тока при параллельном соединении различных приемников. Научиться строить векторно-лучевые диаграммы токов, треугольники токов, проводимостей и мощностей. Изучить явление резонанса токов.

2.2. Для схем рис.6.1а, 6.2а, рис.6.4а, рис.6.6 записать выражения для расчета величин, приведенных в таблицах 1¸4 (результаты вычислений) по показаниям приборов (данные измерений).