








Республика Беларусь
Кафедра «Высшая математика»
«Ряды Фурье»
Выполнил: Проверил:
студент группы ЭТ-21 Преподаватель
Ваниславчик Д. Ю. Васильева Т. И.
Гомель 2010
Задача 1. Дана функция ![]() в интервале [0;π].
Разложить:
в интервале [0;π].
Разложить:
а) в ряд Фурье по синусам; ( рис. 1)
б) в ряд Фурье по косинусам. ( рис. 2 )
Изобразить графически на всей числовой оси сумму S(x) и частичные суммы S₁(x), S₁(x), S₃(x) ряда.
а) по синусам
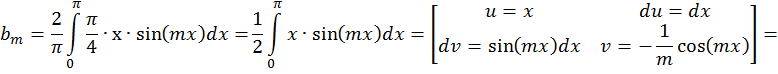
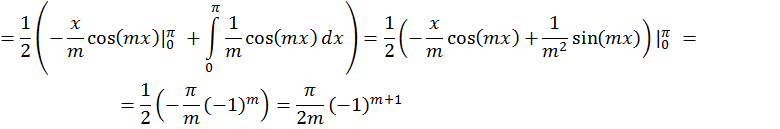
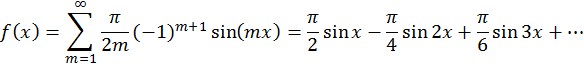
б) по косинусам
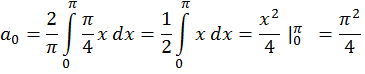
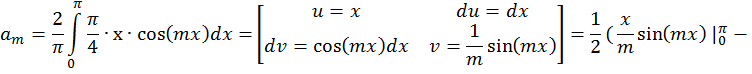
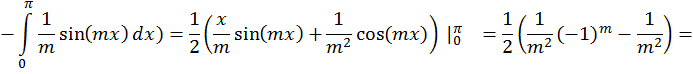
![]()
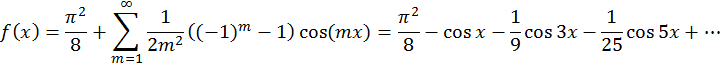
Задача 2. Дана функция ![]() в интервале [0; 3]. Разложить:
в интервале [0; 3]. Разложить:
а) в ряд Фурье по синусам; ( рис. 3)
б) в ряд Фурье по косинусам. ( рис. 4 )
Изобразить графически на всей числовой оси сумму S(x) и частичные суммы S₁(x), S₁(x), S₃(x) ряда.
а) по синусам
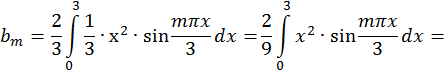
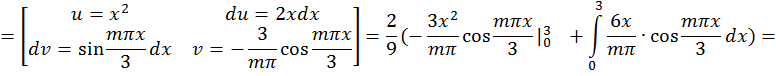
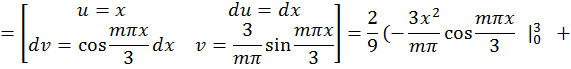
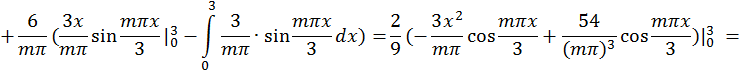
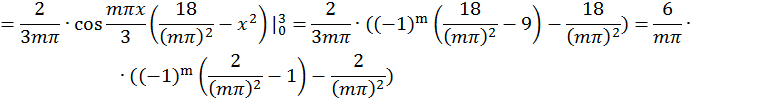
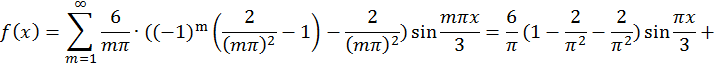
![]()
![]()
б) по косинусам
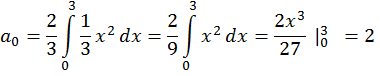
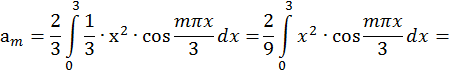
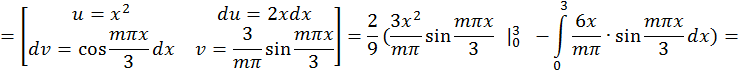
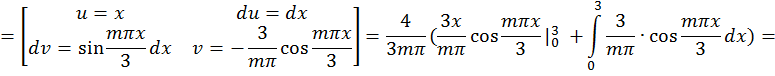
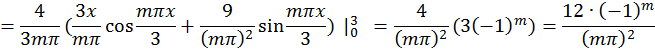
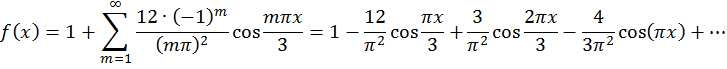
Задача 3. Дана функция 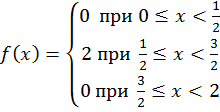 в интервале [0; 2]. Разложить:
в интервале [0; 2]. Разложить:
а) в ряд Фурье по синусам; ( рис. 5)
б) в ряд Фурье по косинусам. ( рис. 6 )
Изобразить графически на всей числовой оси сумму S(x) и частичные суммы S₁(x), S₁(x), S₃(x) ряда.
а) по синусам
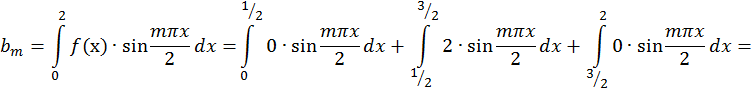
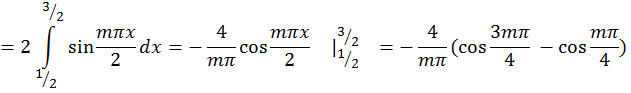
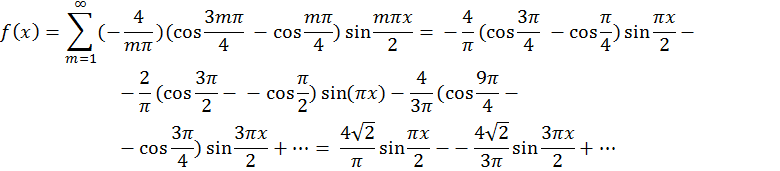
б) по косинусам
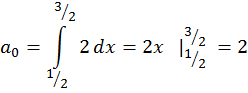
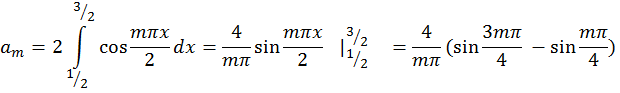
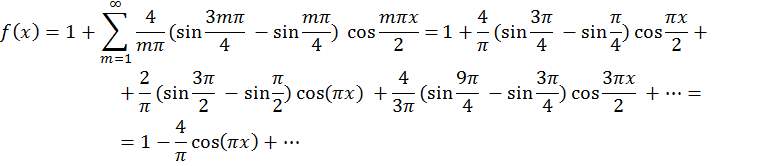
Задача 4. Дана функция ![]() в интервале [0;π].
Разложить:
в интервале [0;π].
Разложить:
а) в ряд Фурье по синусам; ( рис. 7)
б) в ряд Фурье по косинусам. ( рис. 8 )
Изобразить графически на всей числовой оси сумму S(x) и частичные суммы S₁(x), S₁(x), S₃(x) ряда.
а) по синусам
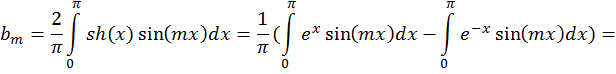
1. ![]()
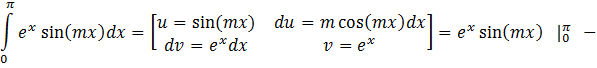
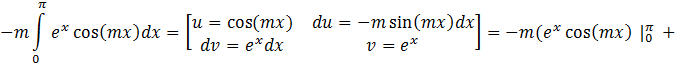
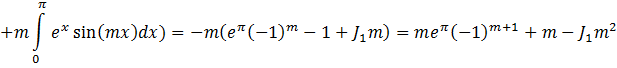
![]()
![]()
2. ![]()
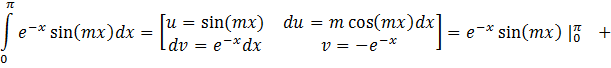
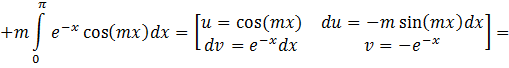
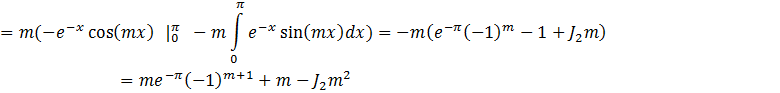
![]()
![]()
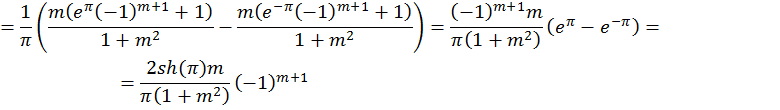
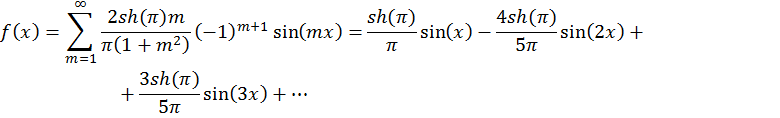
а) по косинусам
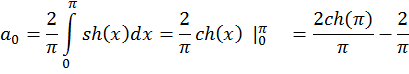
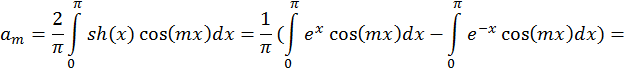
1. ![]()
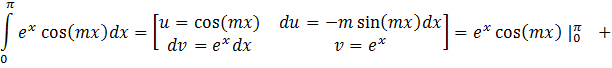
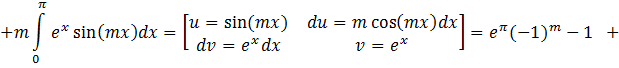
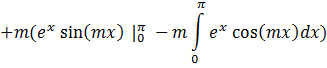
![]()
![]()
2. ![]()
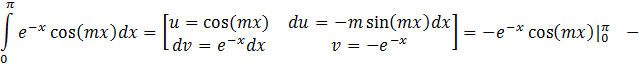
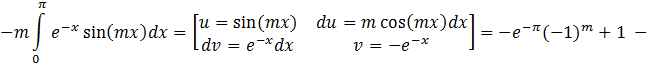
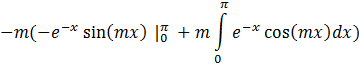
![]()
![]()
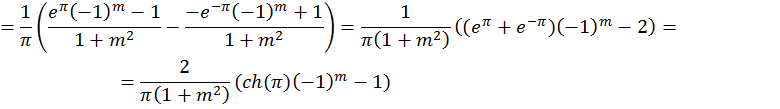
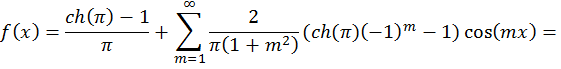
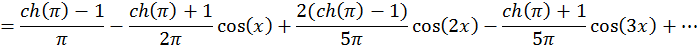
Задача 5. Представить тригонометрическим многочленом третьего порядка функцию f(x), где
|
x |
0 |
|
|
|
|
|
π |
|
|
|
|
|
2π |
|
f(x) |
10 |
30 |
46 |
52 |
46 |
30 |
20 |
30 |
38 |
50 |
40 |
30 |
20 |
#include <math.h>
int main() {
system (“clear”);
float y[]={0,10,30,46,52,46,30,20,30,38,50,40,30,20};
int i, k;
float a[13], b[13], x[13], g[13], s, q, c;
for (i=1; i<=13; i++)
x[i]=s; s=s+M_PI/6;
}
for (i=1; i<=12; i++) q=q+y[i];
q=q/6;
for (k=1; k<=4; k++) {
s=0; c=0;
for (i=1; i<=12; i++) {
s=s+y[i]*cos(k*x[i]);
c=c+y[i]*sin(k*x[i]);
}
a[k]=s/6; b[k]=c/6;
}
printf(“x[i] y[i] g[i] (ответ)\n”);
for (i=1; i<=13; i++) {
g[i]=q/2;
for(k=1; k<=4; k++)
g[i]=g[i]+a[k]*cos(k*x[i])+b[k]*sin(k*x[i]);
printf(“%6.3f %6.0f %6.3f\n”, x[i], y[i], g[i]);
}
return 0;
}
x[i] y[i] g[i] (ответ)
0.000 10 13.333
0.524 30 27.711
1.047 46 47.122
1.571 52 51.854
2.094 46 45.622
2.618 30 30.309
3.142 20 20.333
3.665 30 28.622
4.189 38 40.545
4.712 50 46.479
5.236 40 44.045
5.760 30 26.024
6.283 20 13.333
Задача 6. Разложить в ряд Фурье функцию f(t) периода Т, изображенную на рис.
Выполнить следующие четыре рисунка в
системе координат ![]() , где
, где
![]()
1. Используя основную теорему о разложении функции в ряд Фурье изобразить графически сумму ряда S(t)
2.
Составить первую
частичную сумму ряда ![]() и
и ![]()
3.
Составить вторую
частичную сумму ряда ![]() . Построить
. Построить ![]() и
и ![]() . Сложение гармоник показать на рисунке.
. Сложение гармоник показать на рисунке.
4.
Составить третью
частичную сумму ряда ![]() . Построить
. Построить ![]() и
и ![]() .
.
(Рис.9)
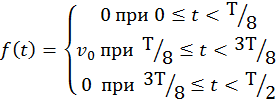
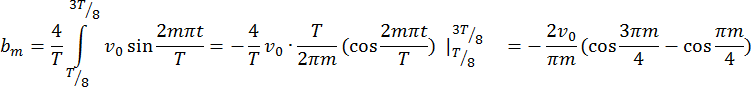
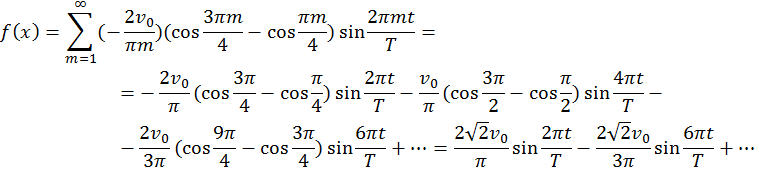
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.