Вычисление координат вершин замкнутого теодолитного хода, выполнение накладок точек на план

Содержание

1. Цель работы.. 2

2. Вычисление дирекционных углов. 3

2.1. Вычисление угловой невязки. 3

2.2. Вычисление дирекционных углов. 3

3. Вычисление координат вершин замкнутого хода. 5

3.1. Вычисление приращения координат. 5

3.2. Вычисление и распределение линейной невязки. 5

3.3. Вычисление координат вершин теодолитного хода. 6

4. Накладка вершин углов теодолитного хода на план. 8

1. Цель работы

Целью расчетно-графической работы №1 является: изучение методики обра-ботки полевых материалов: вычисление координат вершин замкнутого теодолит-ного хода, выполнение накладок точек на план.

2. Вычисление дирекционных углов

2.1. Вычисление угловой невязки

Вычислю угловую невязку в замкнутом ходе, используя формулу:

где   - сумма измеренных углов;  - теоретическая сумма углов, при этом  - сумма внутренних углов замкнутого многоугольника (n – число углов).

Подсчитаю допустимую угловую невязку хода по формуле:

где n – число углов в ходе; n = 5.

Условие  соблюдается, распределяю угловую невязку с обратным знаком на все углы поровну с округлением до  с предпочтением углов, образо-ванных короткими сторонами (II и III углы),  используя формулу:

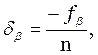
где  - поправка в угол.

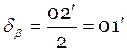
Вычисляю исправленные углы II и III.

Контроль вычисления поправок:

2.2. Вычисление дирекционных углов

Дирекционный угол α – это угол отсчитываемый от положительного (север-ного) направления осевого меридиана до данного направления по ходу часовой стрелки. 0⁰≤α≤360⁰.

Вычисляю дирекционные углы всех сторон хода по исправленном горизон-тальным углам, используя формулу:

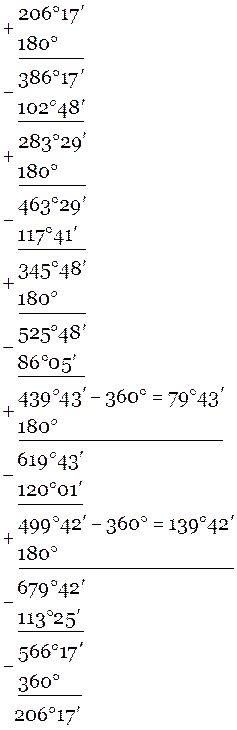
Так как значение  заданное совпадает с полученным значением  в ре-зультате вычислений, делаю вывод, что вычислено правильно.

 3. Вычисление координат вершин замкнутого хода

3.1. Вычисление приращения координат

Вычислю приращения координат  и  по дирекционным углам и гори-зонтальным проложениям сторон теодолитного хода по формулам:

где  - горизонтальное проложение стороны хода;  - дирекционный угол, соответствующий данному направлению.

3.2. Вычисление и распределение линейной невязки

Вычислю линейную невязку, используя формулы:

;      .

;

.

Сравню полученные  и  с допуском:

,

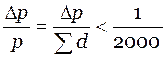 - относительная погрешность.

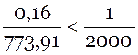- выполняется.

Уравняю ход (распределю линейную невязку) и введу поправки:

,           .

 

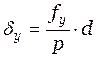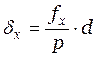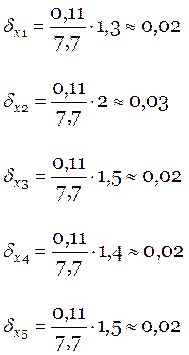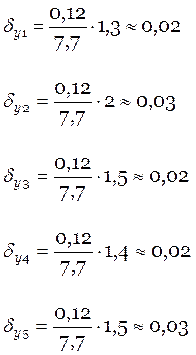В ведомость приращения вписываю с противоположным знаком и рассчиты-ваю исправленные приращения.

Контроль – сумма исправленных приращений по x и y должна быть равна 0.

Вывод: приращения рассчитаны верно.

3.3. Вычисление координат вершин теодолитного хода

Координаты замкнутого теодолитного хода при известной 1-ой координате рассчитываются по формулам:

,

.

 

 

 

По окончании расчётов получил координаты начальной точки  и , что является контролем правильности вычисления.

4. Накладка вершин углов теодолитного хода на план

Накладка теодолитного хода по координатам вершин на план в масштабе 1:2000 начинается с построения координатной сетки. Для её построения применя-ются линейки Дробышева. Это металлическая линейка с вырезами. Края вырезов скошены, на первом из них нанесён индекс «0». Края других вырезов представ-ляют дуги, описанные радиусами 10, 20, 30, 40, и 50 см; конец линейки представ-ляет также дугу радиусом 70, 711 см, что соответствует гипотенузе треугольника с катетами 50х50 см.

Для построения сетки квадратов линейку кладу параллельно нижнему краю листа и тонко отточенным твёрдым карандашом прочерчиваю сначала линию па-раллельно нижнему краю листа, а затем делаю засечки по скошенным краям вы-резов линейки 10, 20, 30 и 40 см на этой линии. Затем таким же образом кладу ли-нейку с правой стороны листа параллельно его краю, совмещаю нулевой указа-тель с последней засечкой (в правом нижнем углу) и по вырезам линейки, начи-ная с первого, прочерчиваю засечки.

После этого проделываю такие же построения слева и с верхней стороны плана, соединяю засечки, получая сетку квадратов. После этого проверяю длину сторон полученных квадратов с помощью масштабной линейки и циркуля-из-мерителя. Расхождение не должно превышать ±0,4 мм.

При нанесении на план точек по прямоугольным координатам прежде всего определяю квадрат, в котором они находятся. Построение произвожу с помощью циркуля-измерителя и масштабной линейки. Каждую точку накладываю и обвожу кружком диаметром 1,5 мм с «усиками» длиной 0,5 мм, слева подписываю номера вершин. Правильность накладки проверяю, сравнивая расстояния между точками с горизонтальным проложением сторон в масштабе плана. Допустимое расхожде-ние ±0,4 мм. 

Работу оформляю в соответствии с образцом и условными знаками.