Информатика и выч. техника \ Прикладная теория цифровых автоматов

Контроль автоматов с памятью, страница 13

Исходя из этого следует выбрать столбцы с одной единицей в них и такие, которые входят в циклы с нечетным числом ребер. В данном случае этому условию удовлетворяют 1 и 7 столбцы. Преобразованный граф переходов показан на рис 22.7.

 


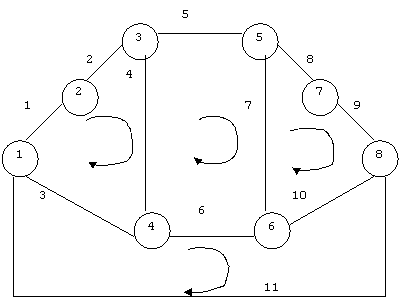Рисунок 22.7 – Граф переходов, допускающий соседнее кодирование состояний

Для преобразованного графа Nф.ц. = 11 – 8 + 1 = 4.

                                     1 2 3 4 5 6 7 8 9 10 11

                              I      1 1 1 1 0 0 0 0 0  0  0    четное

            Мф.ц.=        II     0 0 0 1 1 1 1 0 0  0  0    четное                 (22.4);

                              III    0 0 0 0 0 0 1 1 1 1  0    четное

                              IV    0 0 1 0 0 1 0 0 0 1 1     четное

Следует запомнить, что несмотря на увеличение числа состояний автомата с 6 до 8, количество триггеров в запоминающей части осталось равным трем.

3.  Противогоночное кодирование состояний автомата

Противогоночное кодирование основано на следующем положении:

Допустим требуется исключить критические гонки триггеров на переходе (а, b), связанном с со входным сигналом x1. Из закона функционирования автомата можно определить множество переходов (c1, d1) … (cK, dK) для которых обеспечена возможность выполнения, как и для перехода (а, b). Переход (ci, di) в автомате может выполнятся, как и переход (а, b), если терм из выходных сигналов, связанных с переходом (ci, di) может принимать единичное значение в том случае, если xi=1. Отсутствие критических состязаний на переходе (а, в) может быть обеспечено, если в кодах состояний а, в существует, по крайней мере, одна переменная, принимающая значение в кодах ci, di.

Например, если состояния а, b и ci, di закодированы следующим образом:

Скачать файл