Контроль автоматов с памятью, страница 11

В левой части этого неравенства стоит t_cp^тр – время срабатывания триггера, справа t_зад^кор – время задержки самой короткой цепи. Это способ устранения гонок применим только в том случае, когда триггеры могут переключаться под действием импульсов синхронизации с длительностью t_си.

Недостатком этого способа устранения гонок является сужение возможных пределов изменения длительности t_си. Преимуществом – его простота.

2.  Соседнее кодирование внутренних состояний автомата

Естественно, что гонки в автомате исключены, если при любых переходах изменяется состояние только одного триггера. Этот способ ликвидации гонок ориентирован на устранение первой (основной) причины их возникновения и базируется на использовании специального метода кодирования состояний автомата.

Способ кодирования состояний при котором соседние состояния автомата,

 

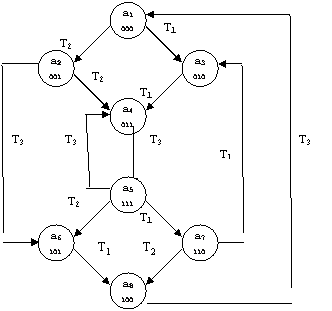Рисунок 22.5 – Граф переходов автомата с соседним кодирование состояний

находящиеся на расстоянии одной дуги графа переходов, различаются состоянием только одного элемента памяти, называется соседним кодирование, приведен на рис. 22.5.

На дугах автомата отмечены сигналы сигналы возбуждения триггеров. Из рис. 22.5 следует, что на любом переходе свое состояние изменяет только один триггер. Однако соседнее кодирование возможно не всегда.

На вопрос, возможно ли соседнее кодирование состояний для данного графа переходов автомата, дает ответ теория графов.

Соседнее кодирование состояний осуществимо только для такого графа переходов автомата, матрицы фундаментальных циклов которого содержит циклы только с четным числом состояний.

Количество циклов N_ф.ц. в матрице фундаментальных циклов (цикломатической матрице) определяется по формуле (22.2)

N_ф.ц. = П_ребер – П_вершин +1  (22.2);

Где П_ребер и П_вершин – число ребер и вершин в графе переходов автомата. Известно, что любой другой цикл (не функциональный) в графе переходов может быть путем сложения по модулю 2 некоторого числа фундаментальных циклов. Рассмотрим граф переходов на рисунке 22.6.