Контроль автоматов с памятью, страница 12

 

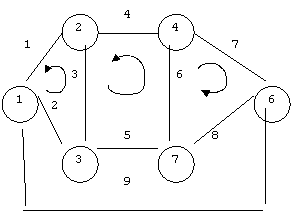
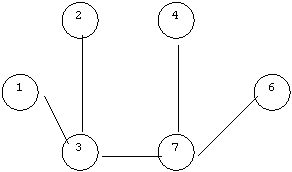
Рисунок 22.6 – Граф переходов автомата и дерево графа

Для построения матрицы фундаментальных циклов следует на нем выделить дерево (остов графа). Деревом называется связанный граф, содержащий все вершины и не содержащий циклов. Как правило на графе можно выделить несколько деревьев. Одно из них приведено на рис. 22.6 б.

Из графа удалены 1, 4, 7 и 9 ребра. Число строк (фундаментальных циклов) N_ф.ц. =9 – 6 + 1 = 4.

В матрице фундаментальных циклов (22.6) строки соответствует номеру цикла, столбцы – номеру ребра. Единицы в столбцах одной строки соответствуют ребрам, образующим соответствующий цикл.

                                     1 2 3 4 5 6 7 8 9

                              I      1 1 1 0 0 0 0 0 0     нечетное

            М_ф.ц.=        II     0 0 1 1 1 1 0 0 0     четное                 (22.3);

                              III    0 0 0 0 0 1 1 1 0     нечетное

                              IV    0 1 0 0 1 0 0 1 1     четное

Так как число единиц в первой и третьей строке М_ф.ц. является нечетным, то соседнее кодирование для данного графа переходов невозможно. Если выполнить операцию сложения по модулю 2 первого и второго циклов получим:

      1 2 3 4 5 6 7 8 9

 I    1 1 1 0 0 0 0 0 0

Å

 II   0 0 1 1 1 1 0 0 0

       1 1 0 1 1 1 0 0 0

Полученный цикл не является фундаментальным, он состоит из ребер 1, 2, 4, 5, 6 и также содержит нечетное число ребер.

Добиться четности всех фундаментальных циклов можно за счет разрыва некоторых ребер и введения дополнительных вершин (дополнительных состояний) в циклы с нечетным числом ребер, чтобы при этом четные циклы не превращались (не преобразовывались) в нечетные.