Горизонтально-ковочная машина: общие сведения. Преимущества и недостатки штамповки на ГКМ, страница 4

, откуда

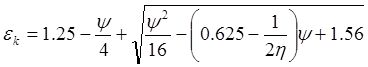  (2)

Данная формула действительна до y £ 11, что соответствует e_k £ 1,25, b < 2,5 и h = 1,05.

Формула (2) является приближенной.

Зависимость e_k=f(y) легко получить из приближенного равенства объемов Vв и Vк также при любой линейной зависимости b =f(e_k), например, в случае использования уточненных экспериментальных данных по правилам высадки.

Для уточнения формулы (2) необходимо сравнить данные, получен­ные по этой формуле с точной зависимостью между e_k и y.

Для получения такой зависимости воспользуемся точным равен­ством объемов Vв = Vк, введя в него l = y  + 2e_k - 5. Имеем

Решив это уравнение относительно y, получим

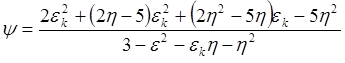 (3)

 

По формуле (3), задаваясь различными e_k при h = 1, легко по­строить кривую e_k = f(y) и сравнить ее с кривой, построенной по фор­муле (2).

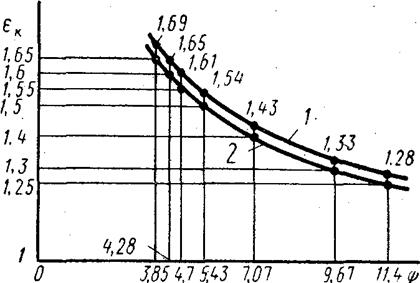           Рис. 13:Кривая зависимости e_k и y.

1 – по формуле (2); 2 – по формуле (3).

Сравнение кривых показывает хорошее совпадение (рис. 13). При e_k в пределах от 1,25 до 1,5 ошибка не превышает 3%. При h>1 ошибка будет еще мень­ше, так как исходное прибли­женное равенство объемов стре­мится к точному при сближении размеров D_k и d_k.

Сравнение кривых показало также, что формулу (2) можно легко скорректировать. Так как

кривые по формулам (2) И (3) эквидистантны, а кривая 1 ле­жит выше кривой 2 на величину 0,03, то достаточно из формулы (2) вычесть 0,03. Тогда получим

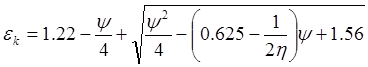  (4)

Формула (4) и является расчетной.

Величину l можно определить, исходя из точной формулы равен­ства объемов Vв = Vк, т. е.

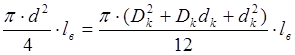
В относительных величинах имеем

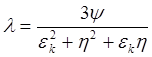
Величину l_k необходимо скорректировать в соответствии с коэф­фициентом увеличения полости U:

l_k.скорр = Ul_k

Обычно h принимают равным 1,05.

Формула (4) применима при 11 > y > 5,4.

При y £ 5,4 e_k принимают равным 1,5, h = 1,05, подсчитывают D_k и d_k и определяют l, а, следовательно, и l_k .

Иногда в наборном коническом пуансоне имеется керн. Тогда мень­ший диаметр конуса d_k должен быть больше 1,1d.

Последующая высадка. При высадке на ограниченный диаметр в матрице или пуансоне (см. рис. 7, 8, 10, 11) может оказаться,

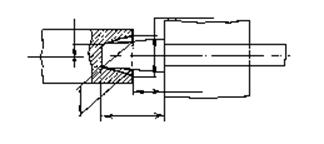Рис. 14: Ограничение выступающей длины предварительно высаженного конического перехода за пределы конического пуансона при D_k£ 1.5d_ср.

что длина высаженной части будет слишком велика по сравнению со средним ее диаметром. В этом слу­чае последующая свободная высад­ка окажется невозможной и не­обходим дополнительный наборный переход. При этом переходы выби­рают однотипными.

Обычно это наборные переходы в конических пуансонах (рис. 14). Если после первого набора длина конуса l_k окажется больше 2,5 d_ср, то необходима вторичная высадка в коническом наборном пуансоне. Средний диаметр можно принять как средний алгебраический

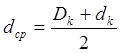
Можно подсчитать также средний диаметр более точно, исходя из равенства объемов конуса Vк и цилиндра, диаметром d_ср1 и длиной, равной длине конуса l_k. Имеем

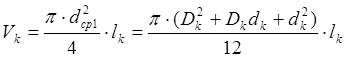
откуда

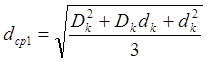
Если сравнить d_ср с d_ср1 при h = 1 и e_k = 1,25, то получим

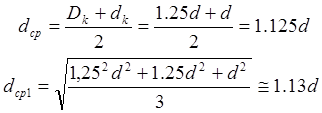
При h = 1 и e_k = 1,5 имеем

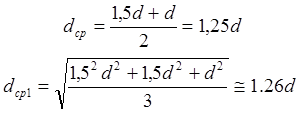
Как видим, d_ср и d_ср.1 в диапазоне e_k от,1,25 до 1,5 примерно равны. Если вместо d_ср принять d_ср1 (которое легко определить), то расчет второго конического наборного пуансона можно проводить аналогично расчету для первого перехода из условий V_k » V_k1 (V_k1 - объем вто­рого конического наборного пуансона) и b = -2e_k - 5.

Для второго наборного пуансона e_k1 = D_k1/d_ср.1, причем D_k1 - больший диаметр конической полости. Величина e_k1 определится по формуле

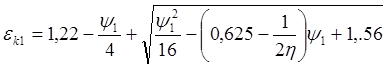  (5)

где

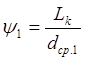
Длина конической полости второго наборного пуансона L_k1 опре­делится из формулы . В свою очередь l₁ можно найти по формуле

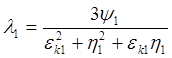  (6)

где

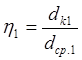
d_к1 — меньший диаметр конической полости второго перехода.

Величина L_к1 в дальнейшем должна быть скорректирована в соот­ветствии с коэффициентом увеличения конической полости U.

Если после второго наборного перехода окажется, что

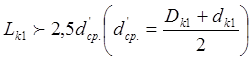
то требуется третий конический наборный переход, расчет которого ана­логичен расчету второго перехода с изменением формул (5) и (6) в со­ответствии с изменением y₁ на .y₂:

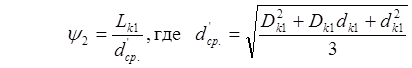
Подобный расчет производят до тех пор, пока значение y не станет равным 2,5 или меньше. Это будет указывать на то, что наборных пере­ходов больше не требуется и можно выполнять окончательную вы­садку фланца в формовочном переходе.