Горизонтально-ковочная машина: общие сведения. Преимущества и недостатки штамповки на ГКМ, страница 3

Если l_B > 11 d, то Dк = 1,25 d, а l₁  = 2,5 d; конструкцию пуансона выполняют в соответствии с рис. 11.

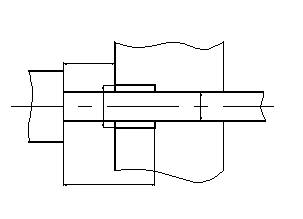Рис. 8 Ограничение выступающей длины прутка при D£1.25d

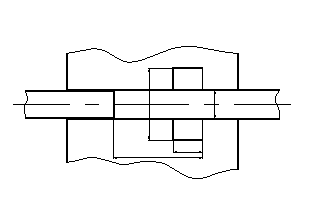Рис.9 Ограничение величены H при высадке прутка во внутренней цилиндрической полости.

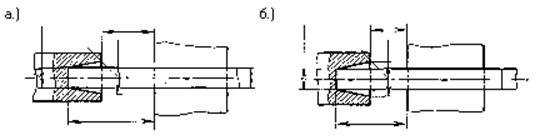Рис. 10: Ограничение выступающей длины прутка за пределы пуансона.

а – при D_k £ 1.5d; б – при D_k £ 1.25d.

Выше были приведены данные, основанные на практике штамповки на ГКМ.

Определение размеров конусных пуансонов при первоначальной высадке. Приведенные практические данные о соотношении размеров заготовки и инструмента при высадке в конических пуансонах не позво­ляют непосредственно по ним выполнить конструкцию пуансона со всеми необходимыми размерами. Для определения рабочих размеров конической полости пуансона необходимо учитывать также очевидное равенство объемов конической полости и высаживаемой части прутка. Объем высаживаемой части прутка определяется по формуле (рис. 12):

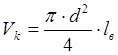
Объем конической полости

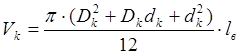
На практике часто задаются размером Dк, принимают dк » d, и, зная, что Vk =V'в=(pd²/4)1в, получают 1в. После этого проверяют, какова окажется длина 1₁ и удовлетворяет ли она вышеупомянутым со­отношениям. Если /₁ оказывается слишком большой, то Dк уменьшают и расчет повторяют снова.

А. Д. Томленов предложил рассчитывать размеры конической по­лости. пуансона, используя упомянутое равенство объемов Vв = Vк и относительные размеры полости и высаживаемой длины прутка (от­носительные величины показаны на рис. 12). Имеем

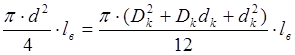
Поделив обе части равенства на d³ и, сделав сокращения, получим в относительных величи­нах следующую формулу:

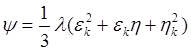
где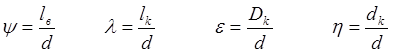

Решая данное уравнение относительно e_k ,получим:

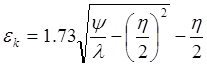  (1)

В формуле (1) l является не­известной величиной, которую можно определить по формуле:

В свою очередь определяется по эмпирической формуле , причем b<3.

Последняя формула дает предельные значения b. Как показала практика, для получения высокого качества поковок, в том числе мак­роструктуры, величина b должна иметь более низкие значения, чем получаемые по данной формуле. Так, при e_k = 1,25 принимают b £ 2,5 и при

e_k =1,5 b£ 2 . Эти максимальные значения приняты в отечественных нормалях машиностроения.

Кроме этого, в формуле (1) не учтена необходимость иметь большую полость в наборном пуансоне по сравнению с полостью формовочной части ручья, что также принято в нормалях. Зависимость b= f(y) менее характерна, чем b= f(e_k). .

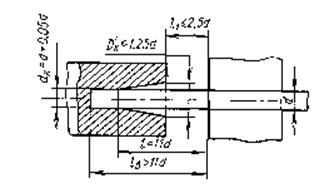Рис. 11: Высадка в коническом пуансоне l_в>11d

 

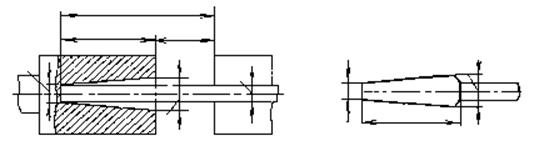Рис. 12: Схема высадки в коническом пуансоне.

Для уточнения расчетов конического пуансона необходимо было получить новую формулу для e_k, которая учитывала бы зависимость b =f(e_k), а последняя соответствовала бы принятым в нормалях рекомендациям. Расчет по такой формуле должен был бы удовлет­ворять условиям равенства объема конической полости V_k объему высаживаемой части прутка V_в, причем 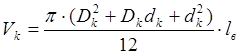  и 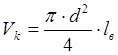, и учитывать необходимость увеличения конической по­лости на величину коэффициента U (U колеблется от 1,02 до 1,13).

Использование формулы (1), которая учитывает равенство объемов конической полости и высаживаемой части прутка, в сочетании с фор­мулой b =f(e_k), невозможно, так как в этом случае получается неяв­ная функция относительно e_k, что приводит к необходимости много­кратных пересчетов.

Учитывая изложенное, была получена новая формула для e_k в зависимости от y, h и U, которые являются известными (или зада­ваемыми) величинами.

Зависимостьb =f(e_k) в первом приближении можно принять линей­ной. Тогда, при b = 2,5

e_k =1,25 и b=2  e_k = 1,5 имеем b =-2e_k + 5.

Однако введение зависимости b =f(e_k) в формулу равенства объе­мов конической полости и высаживаемой части прутка приводит к уравнению выше второй степени относительно e_k и к математическим трудностям в решении уравнения относительно e_k.

Для получения зависимости e_k = f(y, h) с учетом b =f(e_k) представ­ляется целесообразным исходить из приближенного равенства объе­мов Vв и Vк с учетом необходимости увеличения объема полости Vk на величину коэффициента U.

Приняв U = 1, имеем

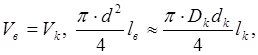
или в относительных величинах,

Учитывая, что l = y - b, имеем

l = y + 2e_k -5

Подставив вместо l ее выражение, получим