









4. Силовой анализ механизма.
Силовой анализ будем проводить как аналитическим, так и графическим методами по следующему алгоритму:
определим силы инерции звеньев
1. выделяем структурные группы Ассура
2. начиная с последней структурной группы, в которую входит начальное звено, последовательно определим реакции во всех кинематических парах;
3. из условия равновесия начального звена найдем уравновешивающий момент и реакцию, действующую на него со стороны стойки.
4.1. Определение сил инерции звеньев.
Согласно принципу Даламбера звено механизма можно рассматривать как находящееся в равновесии, если ко всем внешним силам, действующим на него, добавить силы инерции.
Сила инерции Fи и момент пары сил инерции Ми можно определить по следующим формулам:
FИ=-mias
МИ=-Isei
Где m- масса звена, аs- вектор ускорения центра масс, Js- момент инерции звена относительно оси, проходящей через центр масс перпендикулярно плоскости движения, e- угловое ускорение звена.
Находим для исследуемого механизма угловые ускорения звеньев и линейные ускорения центров масс звеньев в проекциях на оси координат.
Для начального звена в первом положении будет:
аs1=0; e1=-2.0449 1/с2; w1=6.0921 1/с
Для остальных звеньев ускорения центров масс и угловые ускорения находим по формулам, связывающим их с аналогами скоростей и ускорений, которые имеют следующий вид:
аSix=Six''w12+ Six'e1; аSiy=Siy''w12+ Siy'e1 (3.1)
ei=ji''w12+ ji'e1
Ускорение центра масс и угловое ускорение для второго звена примут вид:
аS2x=(-0.15153)·6.09212+(-0.03484)·(-2.0499)=-5.704749 м/с2
аS2y=(-0.02448)·6.09212+(-0.04632)·(-2.0499)=-0.813636 м/с2
e2=0.33974·6.09212+0.39974·(-2.0499)=11.789387 1/с2
аS4x=(-0.21382)·6.09212+(-0.10277)·(-2.0499)=-7.725255 м/с2
аS4y=(0.00432)·6.09212+(-0.012094)·(-2.0499)=0.185287 м/с2
e4=0.08645·6.09212+(-0.0155)·(-2.0499)=3.240125 1/с2
аS5x=(-0.11766)·6.09212+(-0.10509)·(-2.0499)=-4.1516 м/с2
e3=0.47044·6.09212+0.33593·(-2.0499)=16.7715 1/с2
Определив ускорения звеньев, находим главный вектор и главный момент сил инерции звеньев механизма:
Звено 1: Fи1=0 H;
Mи1=-Jo1e1=-1.2·(-2,0499)=2,4598511 H;
Звено 2: Fи2х=-m2·аS2x=-17·(-5,704749)=96,980728 H;
Fи2y=-m2·аS2y=-17·(-0.813636)=13,83182 H;
Mи2=-Js2·e2=-0,5·11.789387=-5.894693 H·м;
Звено 3: Fи3y=0 H;
Fи3x=0 H;
Mи3=-Js3·e3=-1.1·16,7715=-18,44864 H·м;
Звено 4: Fи4x =-m4·аS4x=-90·(-7,725255)=695,2729 H;
Fи4y=-m4·аS4y=-90·0,185287=-16,675872 H;
Mи4=-Js4·e4=-40·3,240125=-129,60499 H·м;
Звено 5: Fи5x =-m5·аS5x=-450·(-4,1516)=1868,2035 H;
Fи5y=0 H;
Mи4=0 H;
|
Силы инерции |
Cилы тяжести |
Сила сопр. |
||||||||||
|
Mи1 |
Fи2х |
Fи2y |
Mи2 |
Mи3 |
Fи4x |
Fи4y |
Mи4 |
Fи5x |
F2y |
F4y |
F5y |
Fc |
|
-2,4598 |
96,9807 |
13,832 |
-5,89469 |
-18,448 |
695,273 |
-16,676 |
-129,6 |
1868,2 |
-166,6 |
-882 |
-4410 |
-4000 |
4.2. Силовой расчет последней присоединенной группы Ассура.
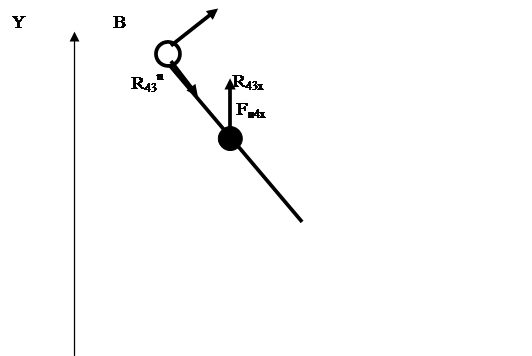
Рассмотрим структурную группу 4-5 .Прикладываем к ней в проекциях на оси, действующие на нее силы. Действие на звено 5 со стороны стойки заменяем реакцией R5d, а на звено 4 со стороны звена 3 реакцией R43.
Записываем в проекциях на оси координат условия равновесия всех сил, действующих на звено 5:
åFX=0
R43n·cos(180-j4)+R43t ·sin(180-j4)+ Fи4x+Fи5x+Fc2=0
åFY=0
R43t·cos(180-j4)+ R43n ·sin(180-j4)+ Fи4y+G4+G5+R50 =0 (3.2)
åMd=0
-R43t·L4+Mи4-Fи4х·L4·0,5·sin(180-j4)-(G4+Fи4y)·(L4/2)·cos(180-j4)=0
R43t
 |

![]()
![]()
![]()
|

![]() Fи5x
Fи5x
![]()
![]()
![]()
![]()
![]() Fc2
Fc2
|
||||||||
|
||||||||
|
||||||||
Решая уравнение (3.2), получим:
R43t=(Mи4/L4)-0,5·Fи4х·sin(180-j4)-0,5·(Fи4y+G4)·cos(180-j4)=0.6737459 H
R43n=(-R43t·sin(180-j4)+Fи4x+Fc2+Fи5x)/cos(180-j4)=-7571.165 H
R50=-[ R43t·cos(180-j4)+R43n·sin(180-j4)+Fи4х+G4+G5]=9086.936 H
R43x= R43t·sin(180-j4) +R43n·cos(180-j4)=-6563.476 H
R43y= R43t·cos(180-j4) +R43n·sin(180-j4)=-3772.9 H
R43=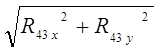 =7570.58
H
=7570.58
H
Реакция R34 является внутренней, она равна по модулю и противо-
положна по направлению внешней реакции R43 и поэтому : R34= -R43.
Для исследуемого положения реакции определятся:
R34=-7570.58 Н R43= 7570.58 Н R50=9086.936 H
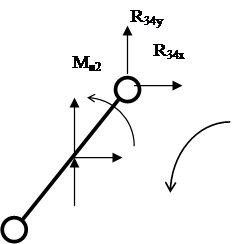
4.3. Силовой расчет первой присоединенной группы Ассура (структурной группы 2-3).
Помимо заданных сил и сил инерции, на группу действуют реакции R34 ,R30 R21. Силы представлены через их проекции на оси координат.
Проекции R34х и R34y были найдены из анализа предыдущей группы.
Для определения реакции в кинематических парах А и С записываем два уравнения проекций на координатные оси и два уравнения моментов относительно точки В:
åМB(3)=Mи3-R30t·Lbc+G3·cos(180°-j3)·Lbc=0
åМB(2)=Mи2-R21t·Lab+(G3+Fи2y)·Lab·0,5·sin(j2-90°)·Lbc+Fи2х·Lab·0,5·
·cos(j2-90°)=0
åFx=R34x+Fи2x+R21t·cos(j2-90°)-R21n·sin(j2-90°)-R30t·sin(180-j3)-R30n·cos(180-j3)=0
åFy= R34y+Fи2y+G2+G3+ R21t·sin(j2-90°)+R21n·cos(j2-90°)-
-R30t·cos(180-j3)+R30n·sin(180-j3)=0
 |
|||||
|
|
 B
B
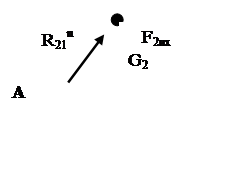 |
|||
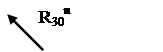 |
|||
|
|
|
G2
Решив уравнения, получим:
R30t =(Mи3/Lab)+G3·cos(j2-90°)=-77.9775 H
R21t=(Mи2/Lоа)+(G2+Fи2y)·0,5·sin(j2-90°)+Fи2х·0,5·cos(j2-90°)=64,89549 H
![]()
R21n·0.503711859-R30n·0.080005989=-6794.24614
R21n·0.863871728+R30n·0.996794382=-3387.464859
Решив систему из двух уравнений, получим:
R30n=7288.098128 Н R21n=-12330.76913 Н
R21х= R21t·cos(j2-90°)- R21n·sin(j2-90°)=-6155.093 H
R21y= R21t·sin(j2-90°)- R21n·cos(j2-90°)=10619.5 H
R21=![]() =12274.3 H
=12274.3 H
R30х= R30t·cos(180°-j3)- R30n·sin(180°-j3)=-7270.974 H
R30y= R30t·sin(180°-j3)- R30n·cos(180°-j3)=-660.82 H
R30=![]() =7300.94 H
=7300.94 H
4.4.Силовой расчет начального звена.( Определение уравновешивающего момента Мy и реакции R10 в кинематической паре А.)
![]() R21y
R21y
![]() А
А
|
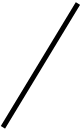

|
 Mур
Mур
|
R12х=-R21х=-6155.093 Н R12y=-R21y=10619.5 H
Для этого составляем уравнения равновесия начального звена механизма:
R10х+ R12х =0
R10y+ R12y=0
Mи1+Мур+R12y·L1·cosj1+R12x·L1·sinj1=0
Решая уравнения, найдем:
R10х=-R21y=6155.093 H R10y=-R12y=-10619.5 H
Myp=-Mи1-R12y·L1·cosj1-R12x·L1·sinj1=706.3403 H·м
4.5. Силовой анализ структурной группы 4-5 графическим методом.
Рисуем структурную группу 4-5 и прикладываем к ней все известные силы и моменты. Под действием приложенных сил и сил реакций структурная группа находится в равновесии. Необходимо определить реакции R50 и R43 во внешних кинематических парах, а также реакцию R45 во внутренней кинематической паре D.
Определим реакции R50 и R43 из условия равновесия звеньев 4-5. Для этого запишем уравнение моментов относительно точки D:
R43t·L4+Mи4+ Fи4х·L4·0,5·sin(180-j4)+(Fи4y+G4)·cos(180-j4)=0
Находим R43t:
R43t=(Mи4/L4)-0,5·Fи4х·sin(180-j4)-0,5·(Fи4y+G4)·cos(180-j4)
R43t+ R43n+Fи4х+ Fи4y+ R50+Fc2+G5+ Fи5х=0 (3.4)
Уравнение (3.4) решаем графическим методом построения планов сил. Выбираем масштабный коэффициент сил mF=100Н/мм. Находим для известных сил величины отрезков, которыми они изображаются на плане сил. Силы Fс, Fи4х, Fи5x
Действуют по одной линии поэтому для них (с учетом знаков
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.